Back to the topics list

معادلات خطی

معادله خطی معادله ای برای یک خط مستقیم است. مثال: 2x + y = 5 یک معادله خطی است

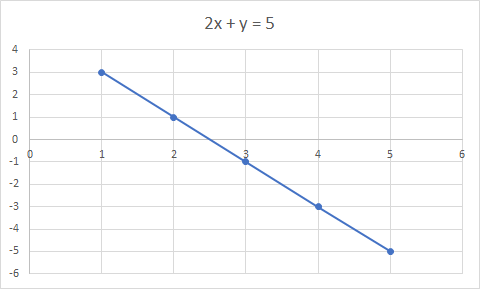
نمودار 2x + y = 5 یک خط مستقیم است

می توانیم معادله خطی را به صورت زیر تعریف کنیم:

معادله خطی معادله ای با درجه 1 است و از این رو یک خط مستقیم را در یک نمودار نشان می دهد. معادلات خطی را معادلات درجه اول نیز می نامند، زیرا بالاترین توان متغیر در این معادلات 1 است.

چگونه بگوییم یک معادله خطی است یا نه؟ بیایید این را با چند مثال در زیر درک کنیم.

مثال:

• 2x + 3y = 5

هر معادله ای درجه دارد. 2x +3y = 5 دارای سه جمله است. بالاترین توان متغیر در یک معادله «درجه» است. در اینجا 2x است، x دارای توان 1 یعنی x ¹ است. در 3y، y نیز توان 1 یعنی y ¹ است، بنابراین این معادله یک معادله خطی است.

• 2x + 3y + 5xy = 10

در این معادله درجه عبارت 5xy دو است. x توان 1 و y توان 1 است بنابراین مجموع درجه که مجموع توان همه متغیرهای آن عبارت است 1 + 1 = 2 است. بنابراین، این معادله یک معادله خطی نیست .

• 2x + 3y + 7z + 9c = 20

در این معادله 5 جمله وجود دارد اما درجه همه این جمله ها 1 است بنابراین این یک معادله خطی است.

در اینجا آموختیم که برای یک معادله خطی هیچ محدودیتی در تعدادی از متغیرهای معادله وجود ندارد. محدودیت در بالاترین توانی است که یک عبارت در یک معادله می تواند داشته باشد.

• \(\mathbf{\frac{2}{x} + y = 10}\)

در این معادله، توان x برابر 1- است (x ^-1 )، بنابراین این معادله یک معادله خطی نیست .

حل معادلات خطی همزمان در دو متغیر

یک سیستم از دو معادله ثابت و مستقل در دو متغیر به صورت زیر حل می شود:
حل:
11x − 7y = 13 …(من)
x − 7y = 3 … (ii)  

روش:

1. یکی از مجهولات را حذف کنید ( بیایید y را حذف کنیم) .
2. مجهول دیگر را حل کنید ( در اینجا x است ).
3. مقدار مجهول حذف شده قبلی را بیابید ( مقدار y را بیابید )

برای حذف یکی از ناشناخته ها (مرحله 1) می توان از روش های زیر استفاده کرد:

• روش تعویض
• روش جمع یا تفریق

روش تعویض:
اجازه دهید با استفاده از این روش معادلات بالا را حل کنیم.
برای (من) 11x − 7y = 13 می گیریم
−7y = 13 − 11x
\(y = \frac{(13 - 11x)}{-7} \)
مقدار y را در معادله دوم جایگزین کنید.
x − 7y = 3
\(x - 7(\frac{13 - 11x}{-7}) = 3 \)
x + 13 − 11x = 3
−10x = 3 − 13
−10x =−10
بنابراین، x = 1
به عنوان \(y = \frac{(13 - 11x)}{-7} \) ، مقدار x را در اینجا جایگزین کنید و مقدار y را بدست آورید
\(y = \frac{13 - (11 \times 1)}{-7}\)
\(y = \frac{13 - 11}{-7} \\ y = \frac{-2}{7}\)
بنابراین، x = 1 و y = -2 ∕ 7 راه حل مورد نیاز است.

روش حذف:
حل:
2x + 3y = 10
x + y = 6

1. با ضرب هر دو معادله در یک عدد، ضریب یک متغیر را در هر دو معادله یکسان کنید (مثلا y).
   (2x + 3y = 10) × 1
   ( x + y = 6 ) × 3
   اکنون هر دو معادله دارای ضریب y برابر با 3 هستند.
2. برای خلاص شدن از شر یک متغیر، اضافه یا تفریق کنید و سپس معادله را تنها با یک متغیر حل کنید (حل x)
   2x + 3y = 10
   3x + 3y = 18
   معادله دوم را از معادله اول کم کنید.
   +2x + 3y =+10
   +3x + 3y = +18
   ----
   ------------------
   −x = -8
   بنابراین، x = 8
   y = 6 − x ⇒ y = 6 − 8 = −2
   بنابراین x = 8، y = -2

مسائل کلمه ای که شامل معادلات همزمان است:

مثال 1 : مجموع ارقام یک عدد دو رقمی معین 13 و عدد 2 بیشتر از 7 برابر رقم واحد است. اعداد را پیدا کنید
فرض کنید x در محل واحد و y در مکان ده ها قرار گیرد.
10y + x = عدد = yx
y + x = 13
10y + x = 2 + 7x ⇒ 10y − 6x = 2
2(5y −3x) = 2 ⇒ 5y − 3x = 1 ⇒ \( y = \frac{1 + 3x}{5}\) … با استفاده از روش جایگزینی
y + x = 13 ⇒ \(\frac{1 + 3x}{5} + x = 13\)
1 + 3x + 5x = 13 × 5
1 + 8x = 65 ⇒ 8x = 64
x = 8، بنابراین y = 13 - x ⇒ y = 13 - 8 = 5
عدد 10 × 5 + 8 = 58 است (پاسخ)

مثال 2: هزینه 3 قوطی قهوه و 2 بسته چای 15 دلار و یک قوطی قهوه و 4 بسته چای از همان نوع 12 دلار است. هزینه هر کدام را بیابید.
بگذارید هزینه یک قوطی قهوه x $ و برای یک بسته چای y $ باشد.
3x + 2y = 16
1x + 4y = 12
از روش حذف استفاده کنید،
12x + 8y = 64
+2x + 8y = 24
----
----------------
10x = 40
x = 4، بنابراین 4 + 4y = 12 ⇒ y = 2
هزینه یک قوطی قهوه 4 دلار و هزینه یک بسته چای 2 دلار است.(پاسخ)