Back to the topics list

équations linéaires

Une équation linéaire est une équation pour une ligne droite. Exemple : 2x + y = 5 est une équation linéaire

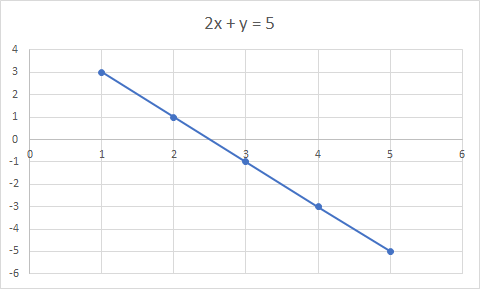
Le graphique de 2x + y = 5 est une droite

Nous pouvons définir une équation linéaire comme :

L'équation linéaire est une équation de degré 1 et représente donc une ligne droite sur un graphique. Les équations linéaires sont également appelées équations du premier degré , car la puissance la plus élevée de la variable dans ces équations est 1.

Comment dit-on si une équation est linéaire ou non ? Comprenons cela avec quelques exemples donnés ci-dessous.

Exemple:

• 2x + 3a = 5

Toute équation a un degré. 2x +3y = 5 a trois termes. La puissance la plus élevée de la variable dans une équation est le « degré ». Voici 2x, x a une puissance 1 soit x ¹ . En 3y, y est aussi de puissance 1 soit y ¹ , donc cette équation est une équation linéaire

• 2x + 3y + 5xy = 10

Dans cette équation, le degré du terme 5xy est deux. x est de puissance 1 et y est de puissance 1, donc le degré total, qui est la somme de la puissance de toutes les variables de ce terme, est 1 + 1 = 2. Par conséquent, cette équation n'est pas une équation linéaire.

• 2x + 3a + 7z + 9c = 20

Dans cette équation, il y a 5 termes mais le degré de tous ces termes est 1, donc c'est une équation linéaire.

Ici, nous avons appris que pour une équation linéaire, il n'y a pas de limitation sur un nombre de variables dans l'équation. La limitation porte sur la puissance la plus élevée qu'un terme d'une équation peut avoir.

• \(\mathbf{\frac{2}{x} + y = 10}\)

Dans cette équation, la puissance de x est -1 (x ^-1 ), donc cette équation n'est pas une équation linéaire.

Résolution d'équations linéaires simultanées à deux variables

Un système de deux équations cohérentes et indépendantes à deux variables est résolu comme suit :
Résoudre:
11x − 7y = 13 …(je)
x - 7y = 3 …(ii)  

Méthode:

1. Éliminer l'une des inconnues( éliminons y) .
2. Résolvez pour l'autre inconnue ( ici c'est x ).
3. Trouver la valeur de l'inconnue éliminée précédemment( trouver la valeur de y )

Pour éliminer l'une des inconnues (étape 1), les méthodes suivantes peuvent être utilisées :

• Méthode de remplacement
• Méthode d'addition ou de soustraction

Méthode de remplacement :
Résolvons les équations ci-dessus en utilisant cette méthode.
Pour (je) on obtient 11x − 7y = 13
−7y = 13 − 11x
\(y = \frac{(13 - 11x)}{-7} \)
Remplacez la valeur de y dans la deuxième équation.
x - 7y = 3
\(x - 7(\frac{13 - 11x}{-7}) = 3 \)
x + 13 − 11x = 3
−10x = 3 − 13
−10x =−10
Par conséquent, x = 1
as \(y = \frac{(13 - 11x)}{-7} \) , remplacez la valeur de x ici et obtenez la valeur de y
\(y = \frac{13 - (11 \times 1)}{-7}\)
\(y = \frac{13 - 11}{-7} \\ y = \frac{-2}{7}\)
Par conséquent, x = 1 et y = −2 ∕ 7 est la solution requise.

Méthode d'élimination :
Résoudre:
2x + 3a = 10
x + y = 6

1. Rendez le coefficient d'une variable dans les deux équations identique (disons y) en multipliant les deux équations par un nombre.
   (2x + 3y = 10) × 1
   ( X + y = 6 ) × 3
   Les deux équations ont maintenant un coefficient de y égal à 3.
2. Additionnez ou soustrayez pour vous débarrasser d'une variable, puis résolvez l'équation avec une seule variable restante (résoudre pour x)
   2x + 3a = 10
   3x + 3a = 18
   Soustrayez la deuxième équation de la première équation.
   +2x + 3a =+10
   +3x + 3a = +18
   - - -
   ------------------
   −x = -8
   Par conséquent, x = 8
   y = 6 − X ⇒ y = 6 − 8 = −2
   Donc x = 8, y = -2

Problèmes écrits impliquant des équations simultanées :

Exemple 1 : La somme des chiffres d'un certain nombre à deux chiffres est 13 et le nombre est 2 plus de 7 fois le chiffre de l'unité. Trouvez les chiffres.
Soit x à la place des unités et y à la place des dizaines.
10y + x = le nombre=yx
y + x = 13
10y + x = 2 + 7x ⇒ 10y − 6x = 2
2(5y −3x) = 2 ⇒ 5y − 3x = 1 ⇒ \( y = \frac{1 + 3x}{5}\) … en utilisant la méthode de substitution
y + x = 13 ⇒ \(\frac{1 + 3x}{5} + x = 13\)
1 + 3x + 5x = 13 × 5
1 + 8x = 65 ⇒ 8x = 64
x = 8, donc y = 13 − x ⇒ y = 13 − 8 = 5
Le nombre est 10 × 5 + 8 = 58 (Réponse)

Exemple 2 : Le coût de 3 boîtes de café et de 2 sachets de thé est de 15 $ et celui d'une boîte de café et de 4 sachets de thé du même type est de 12 $. Trouvez le coût de chacun.
Soit le coût d'une boîte de café est de x $ et pour un paquet de thé est de y $.
3x + 2a = 16
1x + 4a = 12
Utiliser la méthode d'élimination,
12x + 8a = 64
+2x + 8a = 24
- - -
----------------
10x = 40
x = 4, donc 4 + 4y = 12 ⇒ y = 2
Le coût d'une boîte de café est de 4 $ et le coût d'un paquet de thé est de 2 $. (Réponse)