Back to the topics list

linearne jednadžbe

Linearna jednadžba je jednadžba za ravnu liniju. Primjer: 2x + y = 5 je linearna jednadžba

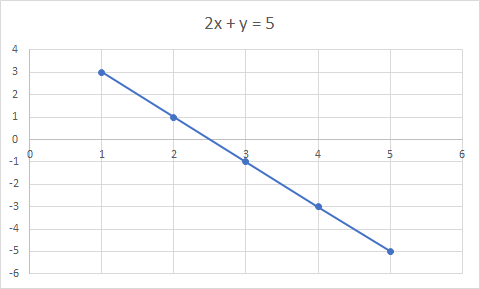
Graf od 2x + y = 5 je ravna linija

Linearnu jednadžbu možemo definirati kao:

Linearna jednadžba je jednadžba prvog stupnja i stoga predstavlja ravnu liniju na grafikonu. Linearne jednadžbe se također nazivaju jednadžbama prvog stupnja , jer je najveća snaga varijable u tim jednadžbama 1.

Kako možemo reći je li jednadžba linearna ili nije? Shvatimo ovo uz pomoć nekoliko primjera u nastavku.

Primjer:

• 2x + 3y = 5

Svaka jednadžba ima stupanj. 2x +3y = 5 ima tri člana. Najveća snaga varijable u jednadžbi je 'stupanj'. Ovdje je 2x, x ima potenciju 1 tj. x ¹ . U 3y, y je također snage 1, tj. y ¹ , stoga je ova jednadžba linearna jednadžba

• 2x + 3y + 5xy = 10

U ovoj jednadžbi, stupanj člana 5xy je dva. x je snage 1, a y je snage 1, tako da je ukupni stupanj, koji je zbroj snaga svih varijabli tog člana, 1 + 1 = 2. Stoga ova jednadžba nije linearna jednadžba.

• 2x + 3y + 7z + 9c = 20

U ovoj jednadžbi postoji 5 članova, ali je stupanj svih ovih članova 1, stoga je ovo linearna jednadžba.

Ovdje smo naučili da za linearnu jednadžbu ne postoji ograničenje broja varijabli u jednadžbi. Ograničenje je najveće snage koju član u jednadžbi može imati.

• \(\mathbf{\frac{2}{x} + y = 10}\)

U ovoj jednadžbi, snaga x je -1 (x ^-1 ), stoga ova jednadžba nije linearna jednadžba.

Rješavanje simultanih linearnih jednadžbi u dvije varijable

Sustav dviju konzistentnih i neovisnih jednadžbi u dvije varijable rješava se na sljedeći način:
Riješiti:
11x − 7y = 13 …(i)
x − 7y = 3 …(ii)  

metoda:

1. Eliminirajte jednu od nepoznanica ( eliminirajmo y) .
2. Riješite drugu nepoznatu ( ovdje je x ).
3. Pronađite vrijednost prethodno eliminirane nepoznate ( nađite vrijednost y )

Za uklanjanje jedne od nepoznatih (korak 1) mogu se koristiti sljedeće metode:

• Metoda zamjene
• Metoda zbrajanja ili oduzimanja

Metoda zamjene:
Riješimo gornje jednadžbe ovom metodom.
Za (i) dobivamo 11x − 7y = 13
−7y = 13 − 11x
\(y = \frac{(13 - 11x)}{-7} \)
Zamjena vrijednosti y u drugoj jednadžbi.
x − 7y = 3
\(x - 7(\frac{13 - 11x}{-7}) = 3 \)
x + 13 − 11x = 3
−10x = 3 − 13
−10x =−10
Stoga je x = 1
kao \(y = \frac{(13 - 11x)}{-7} \) , zamijenite vrijednost x ovdje i dobijte vrijednost y
\(y = \frac{13 - (11 \times 1)}{-7}\)
\(y = \frac{13 - 11}{-7} \\ y = \frac{-2}{7}\)
Dakle, x = 1 i y = −2 ∕ 7 je traženo rješenje.

Metoda eliminacije:
Riješiti:
2x + 3y = 10
x + y = 6

1. Neka koeficijent varijable u obje jednadžbe bude isti (recimo y) množenjem obje jednadžbe s brojem.
   (2x + 3y = 10) × 1
   ( x + y = 6 ) × 3
   Obje jednadžbe sada imaju koeficijent y kao 3.
2. Dodajte ili oduzmite da biste se riješili jedne varijable, a zatim riješite jednadžbu sa samo jednom preostalom varijablom (riješite za x)
   2x + 3y = 10
   3x + 3y = 18
   Oduzmite drugu jednadžbu od prve jednadžbe.
   +2x + 3y =+10
   +3x + 3y = +18
   - - -
   ------------------
   −x = -8
   Stoga je x = 8
   y = 6 − x ⇒ y = 6 − 8 = −2
   Stoga je x = 8, y = -2

Problemi s riječima koji uključuju simultane jednadžbe:

Primjer 1 : Zbroj znamenki određenog dvoznamenkastog broja je 13, a broj je 2 veći od 7 znamenki jedinice. Pronađite brojeve.
Neka je x na mjestu jedinice, a y na mjestu desetica.
10y + x = broj=yx
y + x = 13
10y + x = 2 + 7x ⇒ 10y − 6x = 2
2(5y −3x) = 2 ⇒ 5y − 3x = 1 ⇒ \( y = \frac{1 + 3x}{5}\) … koristeći metodu zamjene
y + x = 13 ⇒ \(\frac{1 + 3x}{5} + x = 13\)
1 + 3x + 5x = 13 × 5
1 + 8x = 65 ⇒ 8x = 64
x = 8, stoga je y = 13 − x ⇒ y = 13 − 8 = 5
Broj je 10 × 5 + 8 = 58 (odgovor)

Primjer 2: Cijena 3 limenke kave i 2 paketa čaja je 15 USD, a cijena jedne limenke kave i 4 paketa čaja iste vrste je 12 USD. Pronađite cijenu svakog.
Neka je cijena jedne limenke kave $x, a jednog paketa čaja $y.
3x + 2y = 16
1x + 4y = 12
Koristite metodu eliminacije,
12x + 8y = 64
+2x + 8y = 24
- - -
----------------
10x = 40
x = 4, stoga je 4 + 4y = 12 ⇒ y = 2
Cijena jedne limenke kave je 4 dolara, a cijena jednog paketa čaja je 2 dolara. (Odgovor)