Back to the topics list

persamaan linear

Persamaan Linear adalah persamaan garis lurus. Contoh: 2x + y = 5 adalah persamaan linier

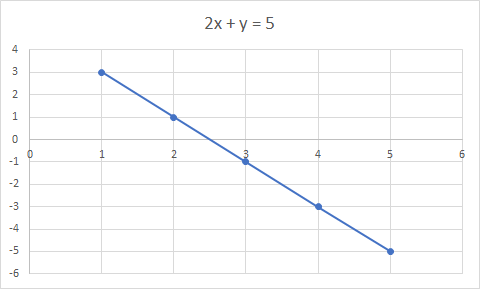
Grafik 2x + y = 5 adalah garis lurus

Kita dapat mendefinisikan Persamaan Linier sebagai:

Persamaan Linear adalah Persamaan derajat 1 dan karenanya mewakili garis lurus pada grafik. Persamaan Linear juga disebut sebagai persamaan derajat pertama , karena pangkat tertinggi dari variabel dalam persamaan ini adalah 1.

Bagaimana kita mengatakan jika suatu persamaan itu linier atau tidak? Mari kita pahami ini dengan beberapa contoh yang diberikan di bawah ini.

Contoh:

• 2x + 3y = 5

Persamaan apa pun memiliki derajat. 2x +3y = 5 memiliki tiga suku. Pangkat tertinggi dari variabel dalam persamaan adalah 'derajat'. Berikut adalah 2x, x memiliki kekuatan 1 yaitu x ¹ . Dalam 3y, y juga berpangkat 1 yaitu y ¹ , oleh karena itu persamaan ini adalah persamaan linier

• 2x + 3y + 5xy = 10

Dalam persamaan ini, derajat suku 5xy adalah dua. x berpangkat 1, dan y berpangkat 1 sehingga derajat total, yang merupakan penjumlahan pangkat semua variabel dari suku tersebut adalah 1 + 1 = 2. Oleh karena itu, persamaan ini bukan persamaan linier.

• 2x + 3y + 7z + 9c = 20

Dalam persamaan ini, terdapat 5 suku tetapi derajat dari semua suku tersebut adalah 1, oleh karena itu persamaan ini adalah persamaan linier.

Di sini kita belajar bahwa untuk Persamaan Linear tidak ada batasan jumlah variabel dalam persamaan. Keterbatasannya adalah pada pangkat tertinggi yang dapat dimiliki suatu suku dalam persamaan.

• \(\mathbf{\frac{2}{x} + y = 10}\)

Dalam persamaan ini, pangkat x adalah -1 (x ^-1 ), sehingga persamaan ini bukan merupakan persamaan linier.

Memecahkan Persamaan Linear Simultan dalam Dua Variabel

Sistem dua persamaan yang konsisten dan independen dalam dua variabel diselesaikan sebagai berikut:
Menyelesaikan:
11x − 7y = 13 …(Saya)
x − 7y = 3 …(ii)  

Metode:

1. Hilangkan salah satu yang tidak diketahui ( mari kita hilangkan y) .
2. Selesaikan untuk yang tidak diketahui lainnya ( ini dia x ).
3. Temukan nilai dari yang tidak diketahui dihilangkan sebelumnya ( cari nilai y )

Untuk menghilangkan salah satu dari yang tidak diketahui (langkah 1) metode berikut dapat digunakan:

• Metode substitusi
• Metode Penambahan atau Pengurangan

Metode substitusi:
Mari kita selesaikan persamaan di atas menggunakan metode ini.
Untuk (Saya) kita mendapatkan 11x − 7y = 13
−7y = 13 − 11x
\(y = \frac{(13 - 11x)}{-7} \)
Substitusikan nilai y ke persamaan kedua.
x − 7y = 3
\(x - 7(\frac{13 - 11x}{-7}) = 3 \)
x + 13 − 11x = 3
−10x = 3 − 13
−10x =−10
Oleh karena itu, x = 1
sebagai \(y = \frac{(13 - 11x)}{-7} \) , gantikan nilai x di sini dan dapatkan nilai y
\(y = \frac{13 - (11 \times 1)}{-7}\)
\(y = \frac{13 - 11}{-7} \\ y = \frac{-2}{7}\)
Oleh karena itu, x = 1 dan y = −2 ∕ 7 adalah solusi yang diperlukan.

Metode eliminasi:
Menyelesaikan:
2x + 3y = 10
x + y = 6

1. Jadikan koefisien variabel di kedua persamaan sama (misalkan y) dengan mengalikan kedua persamaan dengan angka.
   (2x + 3y = 10) × 1
   ( x + y = 6 ) × 3
   Kedua persamaan sekarang memiliki koefisien y sebagai 3.
2. Tambahkan atau kurangi untuk menghilangkan satu variabel dan kemudian selesaikan persamaan dengan hanya satu variabel tersisa (selesaikan untuk x)
   2x + 3y = 10
   3x + 3y = 18
   Kurangi persamaan kedua dari persamaan pertama.
   +2x + 3y =+10
   +3x + 3y = +18
   - - -
   ------------------
   −x = -8
   Oleh karena itu, x = 8
   y = 6 − x ⇒ y = 6 − 8 = −2
   Jadi x = 8, y = -2

Soal Kata yang melibatkan persamaan simultan:

Contoh 1 : Jumlah digit suatu bilangan dua digit tertentu adalah 13 dan bilangan tersebut 2 lebihnya dari 7 kali digit satuan. Temukan angkanya.
Misal x di tempat satuan dan y di tempat puluhan.
10y + x = bilangan = yx
y + x = 13
10y + x = 2 + 7x ⇒ 10y − 6x = 2
2(5y −3x) = 2 ⇒ 5y − 3x = 1 ⇒ \( y = \frac{1 + 3x}{5}\) … menggunakan metode substitusi
y + x = 13 ⇒ \(\frac{1 + 3x}{5} + x = 13\)
1 + 3x + 5x = 13 × 5
1 + 8x = 65 ⇒ 8x = 64
x = 8, maka y = 13 − x ⇒ y = 13 − 8 = 5
Jumlahnya adalah 10 × 5 + 8 = 58 (Jawab)

Contoh 2: Harga 3 kaleng kopi dan 2 bungkus teh adalah $15 dan harga satu kaleng kopi dan 4 bungkus teh dengan jenis yang sama adalah $12. Temukan biaya masing-masing.
Misalkan harga satu kaleng kopi adalah $x dan untuk satu bungkus teh adalah $y.
3x + 2y = 16
1x + 4y = 12
Gunakan metode eliminasi
12x + 8y = 64
+2x + 8y = 24
- - -
----------------
10x = 40
x = 4, jadi 4 + 4y = 12 ⇒ y = 2
Harga satu kaleng kopi adalah $4 dan harga satu bungkus teh adalah $2.(Jawab)