Un'equazione lineare è un'equazione per una linea retta. Esempio: 2x + y = 5 è un'equazione lineare
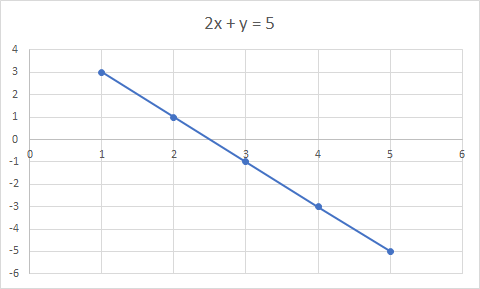
Il grafico di 2x + y = 5 è una linea retta
Possiamo definire un'equazione lineare come:
L'equazione lineare è un'equazione di grado 1 e quindi rappresenta una linea retta su un grafico. Le equazioni lineari sono anche chiamate equazioni di primo grado , poiché la massima potenza della variabile in queste equazioni è 1.
Come si fa a dire se un'equazione è lineare o no? Cerchiamo di capire questo con alcuni esempi riportati di seguito.
Esempio:
Ogni equazione ha un grado. 2x +3y = 5 ha tre termini. La massima potenza della variabile in un'equazione è il "grado". Qui è 2x, x ha una potenza 1 ie x 1 . In 3y, anche y è di potenza 1 ie y 1 , quindi questa equazione è un'equazione lineare
In questa equazione, il grado del termine 5xy è due. x è di potenza 1 e y è di potenza 1 quindi il grado totale, che è la somma delle potenze di tutte le variabili di quel termine è 1 + 1 = 2. Pertanto, questa equazione non è un'equazione lineare.
In questa equazione ci sono 5 termini ma il grado di tutti questi termini è 1, quindi questa è un'equazione lineare.
Qui abbiamo appreso che per un'equazione lineare non vi è alcuna limitazione su un numero di variabili nell'equazione. La limitazione è sulla massima potenza che può avere un termine in un'equazione.
In questa equazione, la potenza di x è -1 (x -1 ), quindi questa equazione non è un'equazione lineare.
Un sistema di due equazioni coerenti e indipendenti in due variabili è risolto come segue:
Risolvere:
11x − 7y = 13
x−7y = 3
Metodo:
Per eliminare uno degli sconosciuti (passaggio 1) è possibile utilizzare i seguenti metodi:
Metodo di sostituzione:
Risolviamo le equazioni di cui sopra usando questo metodo.
Per
−7y = 13 − 11x
\(y = \frac{(13 - 11x)}{-7} \)
Valore sostitutivo di y nella seconda equazione.
x−7y = 3
\(x - 7(\frac{13 - 11x}{-7}) = 3 \)
x+13-11x = 3
−10x = 3−13
−10x = −10
Pertanto, x = 1
come \(y = \frac{(13 - 11x)}{-7} \) , sostituisci qui il valore di x e ottieni il valore di y
\(y = \frac{13 - (11 \times 1)}{-7}\)
\(y = \frac{13 - 11}{-7} \\ y = \frac{-2}{7}\)
Quindi, x = 1 e y = −2 ∕ 7 è la soluzione richiesta.
Metodo di eliminazione:
Risolvere:
2x + 3y = 10
x + y = 6
Esempio 1 : La somma delle cifre di un certo numero a due cifre è 13 e il numero è 2 più di 7 volte la cifra dell'unità. Trova i numeri.
Sia x al posto delle unità e y al posto delle decine.
10y + x = il numero=yx
y + x = 13
10y + x = 2 + 7x ⇒ 10y − 6x = 2
2(5y −3x) = 2 ⇒ 5y − 3x = 1 ⇒ \( y = \frac{1 + 3x}{5}\) … usando il metodo di sostituzione
y + x = 13 ⇒ \(\frac{1 + 3x}{5} + x = 13\)
1 + 3x + 5x = 13 × 5
1 + 8x = 65 ⇒ 8x = 64
x = 8, quindi y = 13 − x ⇒ y = 13 − 8 = 5
Il numero è 10 × 5 + 8 = 58 (Risposta)
Esempio 2: Il costo di 3 barattoli di caffè e 2 bustine di tè è di $15 e quello di un barattolo di caffè e 4 bustine di tè dello stesso tipo è di $12. Trova il costo di ciascuno.
Poniamo che il costo di un barattolo di caffè sia $x e per un pacchetto di tè sia $y.
3x + 2y = 16
1x + 4y = 12
Usa il metodo di eliminazione,
+2x + 8y = 24
- - -
----------------
10x = 40
x = 4, quindi 4 + 4y = 12 ⇒ y = 2
Il costo di un barattolo di caffè è di $ 4 e il costo di un pacchetto di tè è di $ 2. (Risposta)