一次方程式は、直線の方程式です。例: 2x + y = 5 は一次方程式です
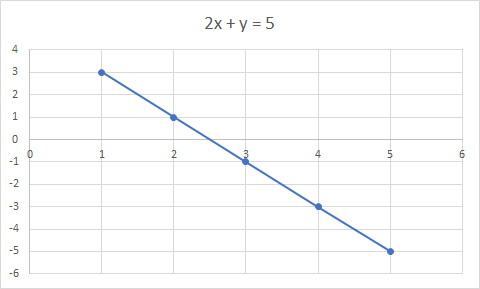
2x + y = 5 のグラフは直線
線形方程式は次のように定義できます。
線形方程式は次数 1 の方程式であるため、グラフ上の直線を表します。線形方程式は、これらの方程式の変数の最大べき乗が 1 であるため、一次方程式とも呼ばれます。
方程式が線形かどうかはどうやって判断するのですか?以下に示すいくつかの例でこれを理解しましょう。
例:
どんな方程式にも次数があります。 2x +3y = 5 には 3 つの項があります。方程式内の変数の最高べき乗は「次数」です。ここに 2x があります。x のべき乗は 1 です。つまり、 x 1です。 3y では、y も 1 乗、つまり y 1なので、この方程式は線形方程式です。
この式では、項 5xy の次数は 2 です。 x は 1 乗、y は 1 乗であるため、その項のすべての変数の累乗の合計である合計次数は 1 + 1 = 2 です。したがって、この方程式は線形方程式ではありません。
この方程式には 5 つの項がありますが、これらすべての項の次数は 1 であるため、これは線形方程式です。
ここで、線形方程式の場合、方程式内の変数の数に制限がないことを学びました。制限は、方程式の項が持つことができる最大のべき乗にあります。
この方程式では、x の累乗は-1 (x -1 ) であるため、この方程式は線形方程式ではありません。
2 つの変数の 2 つの一貫した独立した方程式の系は、次のように解かれます。
解決:
11x − 7y = 13
x − 7y = 3
方法:
不明な (ステップ 1) の 1 つを排除するには、次の方法を使用できます。
置換方法:
この方法で上式を解いてみましょう。
ために
−7y = 13 − 11x
\(y = \frac{(13 - 11x)}{-7} \)
2 番目の式に y の値を代入します。
x − 7y = 3
\(x - 7(\frac{13 - 11x}{-7}) = 3 \)
x + 13 − 11x = 3
−10x = 3 − 13
−10x =−10
したがって、x = 1
\(y = \frac{(13 - 11x)}{-7} \)として、ここに x の値を代入し、y の値を取得します
\(y = \frac{13 - (11 \times 1)}{-7}\)
\(y = \frac{13 - 11}{-7} \\ y = \frac{-2}{7}\)
したがって、x = 1 および y = −2 ∕ 7 が必要な解です。
消去方法:
解決:
2x + 3y = 10
x + y = 6
例 1 :ある 2 桁の数字の桁数の合計が 13 で、その数字が単位の桁の 7 倍より多い 2 です。数字を見つけます。
x を 1 位、y を 10 位とします。
10y + x = 数=yx
y + x = 13
10y + x = 2 + 7x ⇒ 10y − 6x = 2
2(5y −3x) = 2 ⇒ 5y − 3x = 1 ⇒ \( y = \frac{1 + 3x}{5}\) … 置換法を使用
y + x = 13 ⇒ \(\frac{1 + 3x}{5} + x = 13\)
1 + 3x + 5x = 13 × 5
1 + 8x = 65 ⇒ 8x = 64
x = 8 なので y = 13 − x ⇒ y = 13 − 8 = 5
その数は 10 × 5 + 8 = 58 (答え)
例 2:コーヒー缶 3 個とティー パック 2 個の価格は 15 ドルで、同じ種類のコーヒー 缶 1 個とティー パック 4 個の価格は 12 ドルです。それぞれのコストを求めます。
コーヒー缶 1 個の価格を x ドル、ティーパック 1 個の価格を y ドルとします。
3x + 2y = 16
1x + 4y = 12
消去法を使って、
+2x + 8y = 24
- - -
----------------
10x = 40
x = 4 なので 4 + 4y = 12 ⇒ y = 2
コーヒーの缶は 1 缶 4 ドル、ティーパック 1 袋は 2 ドルです。