Линеарна равенка е равенка за права линија. Пример: 2x + y = 5 е линеарна равенка
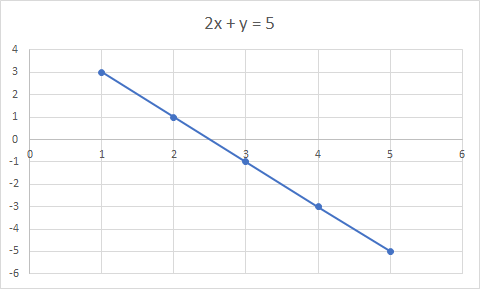
Графикот 2x + y = 5 е права линија
Можеме да дефинираме линеарна равенка како:
Линеарната равенка е равенка од степен 1 и оттука претставува права линија на графикон. Линеарните равенки се нарекуваат и како равенки од прв степен , бидејќи најголемата моќност на променливата во овие равенки е 1.
Како да кажеме дали равенката е линеарна или не? Ајде да го разбереме ова со неколку примери дадени подолу.
Пример:
Секоја равенка има степен. 2x +3y = 5 има три члена. Највисоката моќност на променливата во равенката е „степен“. Еве 2x, x има моќност 1 односно x 1 . Во 3y, y исто така е со моќност 1 т.е. y 1 , затоа оваа равенка е линеарна равенка
Во оваа равенка, степенот на поимот 5xy е два. x е со моќност 1, а y е со моќност 1, така што вкупниот степен, кој е збир на моќноста на сите променливи од тој член е 1 + 1 = 2. Според тоа, оваа равенка не е линеарна равенка.
Во оваа равенка има 5 членови, но степенот на сите овие членови е 1, затоа ова е линеарна равенка.
Овде научивме дека за линеарна равенка нема ограничување на голем број променливи во равенката. Ограничувањето е на највисоката моќност што може да ја има еден член во равенката.
Во оваа равенка, моќта на x е -1 (x -1 ), па оттука оваа равенка не е линеарна равенка.
Систем од две конзистентни и независни равенки во две променливи се решава на следниов начин:
Реши:
11x − 7y = 13
x − 7y = 3
Метод:
За да се елиминира една од непознатите (чекор 1) може да се користат следниве методи:
Метод на замена:
Дозволете ни да ги решиме горните равенки користејќи го овој метод.
За
−7y = 13 − 11x
\(y = \frac{(13 - 11x)}{-7} \)
Заменете ја вредноста на y во втората равенка.
x − 7y = 3
\(x - 7(\frac{13 - 11x}{-7}) = 3 \)
x + 13 − 11x = 3
−10x = 3 − 13
−10x =−10
Затоа, x = 1
како \(y = \frac{(13 - 11x)}{-7} \) , заменете ја вредноста на x овде и добијте ја вредноста на y
\(y = \frac{13 - (11 \times 1)}{-7}\)
\(y = \frac{13 - 11}{-7} \\ y = \frac{-2}{7}\)
Оттука, x = 1 и y = −2 ∕ 7 е потребното решение.
Метод на елиминација:
Реши:
2x + 3y = 10
x + y = 6
Пример 1 : Збирот на цифрите на одреден двоцифрен број е 13, а бројот е 2 повеќе од 7 пати од цифрата на единицата. Најдете ги броевите.
Нека x е на единицата, а y на десетките.
10y + x = бројот=yx
y + x = 13
10y + x = 2 + 7x ⇒ 10y − 6x = 2
2(5y −3x) = 2 ⇒ 5y − 3x = 1 ⇒ \( y = \frac{1 + 3x}{5}\) … користејќи метод на замена
y + x = 13 ⇒ \(\frac{1 + 3x}{5} + x = 13\)
1 + 3x + 5x = 13 × 5
1 + 8x = 65 ⇒ 8x = 64
x = 8, затоа y = 13 − x ⇒ y = 13 − 8 = 5
Бројот е 10 × 5 + 8 = 58 (Одговор)
Пример 2: Цената на 3 калапчиња за кафе и 2 пакетчиња чај е 15 долари, а на еден калај за кафе и 4 пакувања чај од истиот тип е 12 долари. Најдете ги трошоците за секоја од нив.
Нека цената на еден калај кафе е $x, а за едно пакување чај е $y.
3x + 2y = 16
1x + 4y = 12
Користете го методот на елиминација,
+2x + 8y = 24
- - -
----------------
10x = 40
x = 4, затоа 4 + 4y = 12 ⇒ y = 2
Цената на еден калај кафе е 4 долари, а цената на едно пакување чај е 2 долари. (Одговор)