Back to the topics list

linear ညီမျှခြင်း

Linear Equation သည် မျဉ်းဖြောင့်တစ်ခုအတွက် ညီမျှခြင်းတစ်ခုဖြစ်သည်။ ဥပမာ- 2x + y = 5 သည် linear equation ဖြစ်သည်။

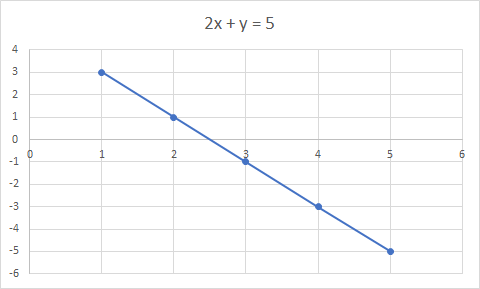
2x + y = 5 ၏ ဂရပ်သည် မျဉ်းဖြောင့်ဖြစ်သည်။

Linear Equation ကို ကျွန်ုပ်တို့ သတ်မှတ်နိုင်သည်-

Linear Equation သည် degree 1 ၏ Equation တစ်ခုဖြစ်ပြီး ထို့ကြောင့် ဂရပ်တစ်ခုပေါ်ရှိ မျဉ်းဖြောင့်ကို ကိုယ်စားပြုသည်။ Linear Equations ကို ပထမဒီဂရီညီမျှခြင်း ဟုလည်း ခေါ်သည်၊ ဤညီမျှခြင်းများတွင် ကိန်းရှင်၏အမြင့်ဆုံးပါဝါသည် 1 ဖြစ်သောကြောင့်ဖြစ်သည်။

ညီမျှခြင်းတစ်ခုသည် linear ဟုတ်မဟုတ် မည်သို့ဆိုမည်နည်း။ အောက်တွင်ဖော်ပြထားသော ဥပမာအနည်းငယ်ဖြင့် ဤအရာကို နားလည်ကြပါစို့။

ဥပမာ-

• 2x + 3y = 5

မည်သည့်ညီမျှခြင်းတွင်မဆို ဘွဲ့တစ်ခုရှိသည်။ 2x +3y = 5 တွင် ဝေါဟာရသုံးမျိုးရှိသည်။ ညီမျှခြင်းတစ်ခုရှိ ကိန်းရှင်၏ အမြင့်ဆုံးစွမ်းအားမှာ 'ဒီဂရီ' ဖြစ်သည်။ ဒီမှာ 2x ၊ x မှာ ပါဝါ 1 ဖြစ်တဲ့ x ¹ ပါ။ 3y တွင် y သည် power 1 ဖြစ်သည့် y ¹ ဖြစ်သည်၊ ထို့ကြောင့် ဤညီမျှခြင်းသည် linear equation ဖြစ်သည်။

• 2x + 3y + 5xy = 10

ဤညီမျှခြင်းတွင် 5xy အခေါ်အဝေါ်၏ ဒီဂရီသည် နှစ်ခုဖြစ်သည်။ x သည် ပါဝါ 1 ဖြစ်ပြီး y သည် ပါဝါ 1 ဖြစ်သောကြောင့် စုစုပေါင်းဒီဂရီဖြစ်ပြီး၊ ထိုကိန်းရှင်အားလုံး၏ ပါဝါပေါင်းချုပ်သည် 1 + 1 = 2 ဖြစ်သည်။ ထို့ကြောင့် ဤညီမျှခြင်းသည် linear equation မဟုတ်ပါ ။

• 2x + 3y + 7z + 9c = 20

ဤညီမျှခြင်းတွင် ကိန်းဂဏန်း 5 လုံးရှိသော်လည်း ဤကိန်းဂဏာန်းအားလုံး၏ အတိုင်းအတာသည် 1 ဖြစ်သောကြောင့် ၎င်းသည် မျဉ်းကြောင်းညီမျှခြင်းဖြစ်ပါသည်။

Linear Equation တစ်ခုအတွက် equation အတွင်းရှိ variable အများအပြားအပေါ် ကန့်သတ်ချက်မရှိကြောင်း ဤနေရာတွင် လေ့လာခဲ့သည်။ ကန့်သတ်ချက်သည် ညီမျှခြင်းတစ်ခုတွင် ကိန်းဂဏန်းတစ်ခုရှိနိုင်သည့် အမြင့်ဆုံးပါဝါ ပေါ်တွင် ဖြစ်သည်။

• \(\mathbf{\frac{2}{x} + y = 10}\)

ဤညီမျှခြင်းတွင် x ၏ ပါဝါသည် -1 (x ^-1 ) ဖြစ်သောကြောင့် ဤညီမျှခြင်းသည် linear equation မဟုတ်ပါ ။

Variable နှစ်ခုဖြင့် တပြိုင်နက်တည်း မျဉ်းသားညီမျှခြင်းများကို ဖြေရှင်းခြင်း။

ကိန်းရှင်နှစ်ခုရှိ တသမတ်တည်းနှင့် အမှီအခိုကင်းသော ညီမျှခြင်းနှစ်ခု၏ စနစ်တစ်ခုကို အောက်ပါအတိုင်း ဖြေရှင်းထားပါသည်။
ဖြေရှင်းရန်-
11x − 7y = 13 …(ဈ)
x − 7y = 3 …(ii)  

နည်းလမ်း-

1. မသိသော အရာများကို ဖယ်ရှားပါ ( y ကို ဖယ်ရှားလိုက်ကြပါစို့) ။
2. အခြားမသိသေးသူများအတွက် ဖြေရှင်းပါ ( ဒီမှာ x )။
3. ယခင်က မသိသော ဖယ်ထုတ်ထားသော တန်ဖိုးကို ရှာပါ ( y တန်ဖိုးကို ရှာပါ )

မသိသေးသော (အဆင့် 1) ကိုဖယ်ရှားရန် အောက်ပါနည်းလမ်းများကို အသုံးပြုနိုင်ပါသည်။

• အစားထိုးနည်း
• ပေါင်းထည့်ခြင်း သို့မဟုတ် နုတ်ခြင်းနည်းလမ်း

အစားထိုးနည်းလမ်း-
အထက်ပါ ညီမျှခြင်းများကို ဤနည်းဖြင့် ဖြေရှင်းကြပါစို့။
ဘို့ (ဈ) 11x − 7y = 13 ကို ရရှိသည်။
−7y = 13 − 11x
\(y = \frac{(13 - 11x)}{-7} \)
ဒုတိယညီမျှခြင်းတွင် y ၏ အစားထိုးတန်ဖိုး။
x − 7y = 3
\(x - 7(\frac{13 - 11x}{-7}) = 3 \)
x + 13 − 11x = 3
−10x = 3 − 13
−10x = −10
ထို့ကြောင့် x = 1
\(y = \frac{(13 - 11x)}{-7} \) အဖြစ်၊ ဤနေရာတွင် x ၏တန်ဖိုးကို အစားထိုးပြီး y တန်ဖိုးကို ရယူပါ။
\(y = \frac{13 - (11 \times 1)}{-7}\)
\(y = \frac{13 - 11}{-7} \\ y = \frac{-2}{7}\)
ထို့ကြောင့် x = 1 နှင့် y = −2 ∕ 7 သည် လိုအပ်သော အဖြေဖြစ်သည်။

ဖယ်ရှားရေးနည်းလမ်း-
ဖြေရှင်းရန်-
2x + 3y = 10
x+y=၆

1. ညီမျှခြင်းနှစ်ခုလုံးရှိ variable တစ်ခု၏ coefficient ကို တူညီအောင်ပြုလုပ်ပါ (y ဆိုကြပါစို့) ညီမျှခြင်းနှစ်ခုလုံးကို ဂဏန်းတစ်ခုဖြင့် မြှောက်ပါ။
   (2x+3y=10)×1
   ( x + y = 6 ) × 3
   ညီမျှခြင်းနှစ်ခုလုံးသည် 3 အဖြစ် y ၏ coefficient ရှိသည်။
2. ကိန်းရှင်တစ်ခုအား ဖယ်ရှားရန် ပေါင်းထည့်ခြင်း သို့မဟုတ် နုတ်ပြီးနောက် ကိန်းရှင်တစ်ခုသာကျန်တော့သော ညီမျှခြင်းအား ဖြေရှင်းပါ (x အတွက် ဖြေရှင်းပါ)
   2x + 3y = 10
   3x + 3y = 18
   ပထမညီမျှခြင်းမှ ဒုတိယညီမျှခြင်းကို နုတ်ပါ။
   +2x + 3y =+10
   +3x + 3y = +18
   - - -
   ------------------
   −x = -၈
   ထို့ကြောင့် x = 8
   y = 6 − x ⇒ y = 6 − 8 = −2
   ထို့ကြောင့် x = 8 ၊ y = -2

တစ်ပြိုင်နက်တည်း ညီမျှခြင်းများ ပါဝင်သော စကားလုံးပြဿနာများ-

ဥပမာ 1 : အချို့သော ဂဏန်းနှစ်လုံး၏ ဂဏန်းများ၏ ပေါင်းလဒ်သည် 13 ဖြစ်ပြီး ဂဏန်းသည် ယူနစ်၏ ဂဏန်းထက် 2 ဆ ပိုများသည်။ နံပါတ်များကိုရှာပါ။
x ကို ယူနစ်နေရာနဲ့ y ဆယ်နေရာမှာ ထားပါစေ။
10y + x = နံပါတ် = yx
y+x=၁၃
10y + x = 2 + 7x ⇒ 10y − 6x = 2
2(5y −3x) = 2 ⇒ 5y − 3x = 1 ⇒ \( y = \frac{1 + 3x}{5}\) … အစားထိုးနည်းလမ်းကို အသုံးပြု၍
y + x = 13 ⇒ \(\frac{1 + 3x}{5} + x = 13\)
1 + 3x + 5x = 13 × 5
1 + 8x = 65 ⇒ 8x = 64
x = 8 ထို့ကြောင့် y = 13 − x ⇒ y = 13 − 8 = 5၊
ဂဏန်းက 10 × 5 + 8 = 58 (အဖြေ)၊

ဥပမာ 2- ကော်ဖီဗူး 3 ဗူးနှင့် လက်ဖက်ရည် 2 ထုပ်၏ ကုန်ကျစရိတ်မှာ $15 ဖြစ်ပြီး ကော်ဖီဗူးတစ်ဗူးနှင့် အမျိုးအစားတူ လက်ဖက်ရည် 4 ထုပ်မှာ $12 ဖြစ်သည်။ တစ်ခုချင်းစီ၏ကုန်ကျစရိတ်ကိုရှာပါ။
ကော်ဖီဗူးတစ်လုံး၏ ကုန်ကျစရိတ်မှာ $x ဖြစ်ပြီး လက်ဖက်ရည်ထုပ်တစ်ထုပ်အတွက် $y ဖြစ်သည်။
3x + 2y = 16
1x + 4y = 12
နှိမ်နှင်းရေးနည်းလမ်းကို အသုံးပြုပြီး၊
12x + 8y = 64
+2x + 8y = 24
- - -
----------------
10x = 40
x = 4 ထို့ကြောင့် 4 + 4y = 12 ⇒ y = 2
ကော်ဖီဗူးတစ်လုံး၏ ကုန်ကျစရိတ်မှာ ၄ ဒေါ်လာဖြစ်ပြီး လက်ဖက်ရည်တစ်ထုပ်၏ ကုန်ကျစရိတ်မှာ ၂ ဒေါ်လာဖြစ်သည်။(အဖြေ)