Back to the topics list

रेखीय समीकरण

एक रेखीय समीकरण एक सीधा रेखा को लागी एक समीकरण हो। उदाहरण: 2x + y = 5 एक रेखीय समीकरण हो

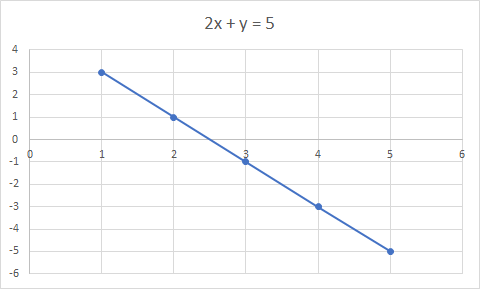
2x + y = 5 को ग्राफ एक सीधा रेखा हो

हामी एक रेखीय समीकरण परिभाषित गर्न सक्छौं:

रेखीय समीकरण डिग्री 1 को एक समीकरण हो र त्यसैले ग्राफ मा एक सीधा रेखा को प्रतिनिधित्व गर्दछ। रैखिक समीकरणहरूलाई पहिलो डिग्री समीकरणहरू पनि भनिन्छ, किनकि यी समीकरणहरूमा चलको उच्चतम शक्ति 1 हो।

समीकरण रेखीय छ वा छैन भनेर हामी कसरी भन्न सक्छौं? तल दिइएका केही उदाहरणहरूद्वारा यसलाई बुझौं।

उदाहरण:

• 2x + 3y = 5

कुनै पनि समीकरणको डिग्री हुन्छ। 2x +3y = 5 मा तीनवटा पदहरू छन्। समीकरणमा चलको उच्चतम शक्ति 'डिग्री' हो। यहाँ 2x छ, x को पावर 1 अर्थात् x ¹ छ। 3y मा, y पनि पावर 1 अर्थात y ¹ को हुन्छ, त्यसैले यो समीकरण एक रेखीय समीकरण हो।

• 2x + 3y + 5xy = 10

यस समीकरणमा, शब्द 5xy को डिग्री दुई छ। x पावर 1 को हो, र y पावर 1 को हो त्यसैले कुल डिग्री, जुन त्यो पदका सबै चरहरूको शक्तिको योगफल हो 1 + 1 = 2। त्यसैले, यो समीकरण रेखीय समीकरण होइन ।

• 2x + 3y + 7z + 9c = 20

यस समीकरणमा ५ वटा पदहरू छन् तर यी सबै पदहरूको डिग्री १ हो, त्यसैले यो एक रेखीय समीकरण हो।

यहाँ हामीले सिकेका छौं कि रेखीय समीकरणको लागि समीकरणमा धेरै चरहरूमा कुनै सीमा छैन। सीमा एक समीकरण मा एक शब्द हुन सक्ने उच्चतम शक्ति मा छ।

• \(\mathbf{\frac{2}{x} + y = 10}\)

यस समीकरणमा, x को शक्ति -1 (x ^-1 ) हो, त्यसैले यो समीकरण रेखीय समीकरण होइन ।

दुई चरहरूमा एकसाथ रैखिक समीकरणहरू समाधान गर्दै

दुई चरहरूमा दुई सुसंगत र स्वतन्त्र समीकरणहरूको प्रणाली निम्नानुसार हल गरिन्छ:
समाधान:
11x − 7y = 13 …(i)
x − 7y = 3 …(ii)  

विधि:

1. अज्ञात मध्ये एक हटाउनुहोस् ( y लाई हटाऔं) ।
2. अन्य अज्ञातका लागि समाधान गर्नुहोस् ( यहाँ यो x हो )।
3. पहिले हटाइएको अज्ञात को मान पत्ता लगाउनुहोस् ( y को मान फेला पार्नुहोस् )

अज्ञात मध्ये एक हटाउन (चरण 1) निम्न विधिहरू प्रयोग गर्न सकिन्छ:

• प्रतिस्थापन विधि
• जोड वा घटाउने विधि

प्रतिस्थापन विधि:
यो विधि प्रयोग गरेर माथिको समीकरणहरू समाधान गरौं।
को लागी (i) हामीले 11x − 7y = 13 पाउँछौं
−7y = 13 − 11x
\(y = \frac{(13 - 11x)}{-7} \)
दोस्रो समीकरणमा y को प्रतिस्थापन मान।
x − 7y = 3
\(x - 7(\frac{13 - 11x}{-7}) = 3 \)
x + 13 − 11x = 3
−10x = 3 − 13
−10x =−10
त्यसैले, x = 1
जस्तै \(y = \frac{(13 - 11x)}{-7} \) , यहाँ x को मान बदल्नुहोस् र y को मान प्राप्त गर्नुहोस्।
\(y = \frac{13 - (11 \times 1)}{-7}\)
\(y = \frac{13 - 11}{-7} \\ y = \frac{-2}{7}\)
त्यसैले, x = 1 र y = −2 ∕ 7 आवश्यक समाधान हो।

उन्मूलन विधि:
समाधान:
2x + 3y = 10
x + y = 6

1. दुवै समीकरणमा एउटा चरको गुणांकलाई समान बनाउनुहोस् (y भनौं) दुवै समीकरणलाई संख्याले गुणन गरेर।
   (2x + 3y = 10) × 1
   ( x + y = 6 ) × 3
   दुबै समीकरणहरूमा अब 3 को रूपमा y को गुणांक छ।
2. एउटा चरबाट छुटकारा पाउन थप्नुहोस् वा घटाउनुहोस् र त्यसपछि मात्र एक चर बायाँको साथ समीकरण समाधान गर्नुहोस् (x को लागि समाधान गर्नुहोस्)
   2x + 3y = 10
   ३x + ३y = १८
   पहिलो समीकरणबाट दोस्रो समीकरण घटाउनुहोस्।
   +2x + 3y =+10
   +3x + 3y = +18
   -----
   ------------------
   −x = -8
   त्यसैले, x = 8
   y = 6 − x ⇒ y = 6 − 8 = −2
   त्यसैले x = 8, y = -2

एकसाथ समीकरणहरू समावेश गर्ने शब्द समस्याहरू:

उदाहरण 1 : निश्चित दुई-अंकको संख्याको अंकहरूको योगफल 13 हो र सङ्ख्या एकाइको अंकको 7 गुणा भन्दा बढी हो। नम्बरहरू फेला पार्नुहोस्।
x लाई एकाइ स्थानमा र y लाई दसको स्थानमा मान्नुहोस्।
10y + x = संख्या = yx
y + x = 13
10y + x = 2 + 7x ⇒ 10y − 6x = 2
2(5y −3x) = 2 ⇒ 5y − 3x = 1 ⇒ \( y = \frac{1 + 3x}{5}\) … प्रतिस्थापन विधि प्रयोग गरेर
y + x = 13 ⇒ \(\frac{1 + 3x}{5} + x = 13\)
1 + 3x + 5x = 13 × 5
1 + 8x = 65 ⇒ 8x = 64
x = 8, त्यसैले y = 13 − x ⇒ y = 13 − 8 = 5
संख्या हो 10 × 5 + 8 = 58 (उत्तर)

उदाहरण 2: 3 कफी टिन र 2 चिया प्याकेट को लागत $15 छ र एक कफी टिन र 4 चिया प्याकेट को समान प्रकार को $12 छ। प्रत्येकको लागत पत्ता लगाउनुहोस्।
एउटा कफी टिनको मूल्य $x हो र एउटा चियाको प्याकेटको लागि $y हो।
3x + 2y = 16
1x + 4y = 12
उन्मूलन विधि प्रयोग गर्नुहोस्,
१२x + ८y = ६४
+2x + 8y = 24
-----
----------------
१०x = ४०
x = 4, त्यसैले 4 + 4y = 12 ⇒ y = 2
एउटा कफी टिनको मूल्य $4 र एउटा चियाको प्याकेटको मूल्य $2 छ। (उत्तर)