Back to the topics list

lineaire vergelijkingen

Een lineaire vergelijking is een vergelijking voor een rechte lijn. Voorbeeld: 2x + y = 5 is een lineaire vergelijking

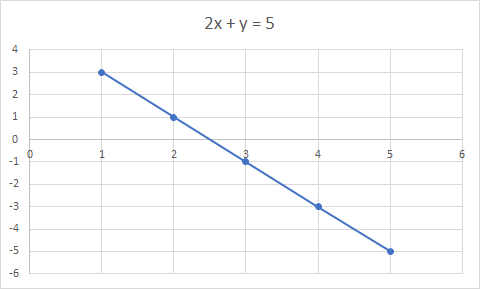
De grafiek van 2x + y = 5 is een rechte lijn

We kunnen een lineaire vergelijking definiëren als:

Lineaire vergelijking is een vergelijking van graad 1 en vertegenwoordigt dus een rechte lijn in een grafiek. Lineaire vergelijkingen worden ook eerstegraadsvergelijkingen genoemd , omdat de hoogste macht van de variabele in deze vergelijkingen 1 is.

Hoe zeggen we of een vergelijking lineair is of niet? Laten we dit begrijpen met een paar voorbeelden hieronder.

Voorbeeld:

• 2x + 3j = 5

Elke vergelijking heeft een graad. 2x +3y = 5 heeft drie termen. De hoogste macht van de variabele in een vergelijking is de 'graad'. Hier is 2x, x heeft een macht 1 dwz x ¹ . In 3y heeft y ook de macht 1, dwz y ¹ , daarom is deze vergelijking een lineaire vergelijking

• 2x + 3j + 5xy = 10

In deze vergelijking is de graad van de term 5xy twee. x is van macht 1, en y is van macht 1, dus de totale graad, die de som is van de macht van alle variabelen van die term, is 1 + 1 = 2. Daarom is deze vergelijking geen lineaire vergelijking.

• 2x + 3j + 7z + 9c = 20

In deze vergelijking zijn er 5 termen, maar de graad van al deze termen is 1, daarom is dit een lineaire vergelijking.

Hier hebben we geleerd dat er voor een lineaire vergelijking geen beperking is op een aantal variabelen in de vergelijking. De beperking ligt bij de hoogste macht die een term in een vergelijking kan hebben.

• \(\mathbf{\frac{2}{x} + y = 10}\)

In deze vergelijking is de macht van x -1 (x ^-1 ), dus deze vergelijking is geen lineaire vergelijking.

Gelijktijdige lineaire vergelijkingen oplossen in twee variabelen

Een stelsel van twee consistente en onafhankelijke vergelijkingen in twee variabelen wordt als volgt opgelost:
Oplossen:
11x − 7y = 13 …(i)
x − 7y = 3 …(ii)  

Methode:

1. Elimineer een van de onbekenden ( laten we y elimineren) .
2. Los op voor de andere onbekende ( hier is het x ).
3. Vind de waarde van de onbekende eerder geëlimineerd ( vind de waarde van y )

Om een van de onbekende (stap 1) te elimineren, kunnen de volgende methoden worden gebruikt:

• Substitutie methode
• Methode voor optellen of aftrekken

Vervangingsmethode:
Laten we de bovenstaande vergelijkingen met deze methode oplossen.
Voor (i) we krijgen 11x − 7y = 13
−7y = 13 − 11x
\(y = \frac{(13 - 11x)}{-7} \)
Vervang de waarde van y in de tweede vergelijking.
x − 7y = 3
\(x - 7(\frac{13 - 11x}{-7}) = 3 \)
x + 13 − 11x = 3
−10x = 3 − 13
−10x =−10
Daarom x = 1
als \(y = \frac{(13 - 11x)}{-7} \) , vervang hier de waarde van x en verkrijg de waarde van y
\(y = \frac{13 - (11 \times 1)}{-7}\)
\(y = \frac{13 - 11}{-7} \\ y = \frac{-2}{7}\)
Daarom is x = 1 en y = −2 ∕ 7 de vereiste oplossing.

Eliminatie methode:
Oplossen:
2x + 3j = 10
x + y = 6

1. Maak de coëfficiënt van een variabele in beide vergelijkingen hetzelfde (laten we zeggen y) door beide vergelijkingen met een getal te vermenigvuldigen.
   (2x + 3y = 10) × 1
   ( x + y = 6 ) × 3
   Beide vergelijkingen hebben nu een coëfficiënt van y als 3.
2. Optellen of aftrekken om één variabele kwijt te raken en vervolgens de vergelijking oplossen met nog maar één variabele over (oplossen voor x)
   2x + 3j = 10
   3x + 3j = 18
   Trek de tweede vergelijking af van de eerste vergelijking.
   +2x + 3j =+10
   +3x + 3j = +18
   - - -
   ------------------
   −x = -8
   Daarom x = 8
   y = 6 − x ⇒ y = 6 − 8 = −2
   Dus x = 8, y = -2

Woordproblemen met gelijktijdige vergelijkingen:

Voorbeeld 1 : De som van de cijfers van een bepaald getal van twee cijfers is 13 en het getal is 2 meer dan 7 keer het cijfer van de eenheid. Zoek de cijfers.
Stel x op de plaats van de eenheid en y op de plaats van de tientallen.
10y + x = het getal=yx
y + x = 13
10y + x = 2 + 7x ⇒ 10y − 6x = 2
2(5y −3x) = 2 ⇒ 5y − 3x = 1 ⇒ \( y = \frac{1 + 3x}{5}\) … met substitutiemethode
y + x = 13 ⇒ \(\frac{1 + 3x}{5} + x = 13\)
1 + 3x + 5x = 13 × 5
1 + 8x = 65 ⇒ 8x = 64
x = 8, dus y = 13 − x ⇒ y = 13 − 8 = 5
Het getal is 10 × 5 + 8 = 58 (Antwoord)

Voorbeeld 2: De kosten van 3 koffieblikken en 2 theezakjes zijn $15 en die van één koffieblik en 4 theezakjes van hetzelfde type $12. Zoek de kosten van elk.
Stel dat de kosten van één koffieblik $x zijn en voor één theezakje $y.
3x + 2j = 16
1x + 4j = 12
Gebruik de eliminatiemethode,
12x + 8j = 64
+2x + 8j = 24
- - -
----------------
10x = 40
x = 4, dus 4 + 4y = 12 ⇒ y = 2
De kosten van een koffieblik zijn $ 4 en de kosten van een theezakje zijn $ 2. (Antwoord)