Back to the topics list

równania liniowe

Równanie liniowe to równanie dla linii prostej. Przykład: 2x + y = 5 to równanie liniowe

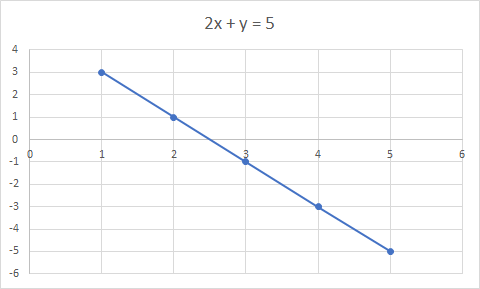
Wykres 2x + y = 5 jest linią prostą

Równanie liniowe możemy zdefiniować jako:

Równanie liniowe jest równaniem stopnia 1, a zatem przedstawia linię prostą na wykresie. Równania liniowe są również nazywane równaniami pierwszego stopnia , ponieważ najwyższa potęga zmiennej w tych równaniach wynosi 1.

Jak stwierdzić, czy równanie jest liniowe, czy nie? Zrozummy to na kilku przykładach podanych poniżej.

Przykład:

• 2x + 3y = 5

Każde równanie ma stopień. 2x +3y = 5 ma trzy wyrazy. Najwyższą potęgą zmiennej w równaniu jest „stopień”. Tutaj jest 2x, x ma potęgę 1, czyli x ¹ . W 3y y również ma potęgę 1, tj. y ¹ , więc to równanie jest równaniem liniowym

• 2x + 3y + 5xy = 10

W tym równaniu stopień wyrazu 5xy wynosi dwa. x jest potęgą 1, a y jest potęgą 1, więc całkowity stopień, który jest sumą potęg wszystkich zmiennych tego wyrazu, wynosi 1 + 1 = 2. Dlatego to równanie nie jest równaniem liniowym.

• 2x + 3y + 7z + 9c = 20

W tym równaniu jest 5 wyrazów, ale stopień wszystkich tych wyrazów wynosi 1, zatem jest to równanie liniowe.

Tutaj dowiedzieliśmy się, że dla równania liniowego nie ma ograniczeń co do liczby zmiennych w równaniu. Ograniczenie dotyczy najwyższej potęgi , jaką może mieć wyraz w równaniu.

• \(\mathbf{\frac{2}{x} + y = 10}\)

W tym równaniu potęga x wynosi -1 (x ^-1 ), stąd to równanie nie jest równaniem liniowym.

Rozwiązywanie równoczesnych równań liniowych z dwiema zmiennymi

Układ dwóch spójnych i niezależnych równań dla dwóch zmiennych rozwiązuje się w następujący sposób:
Rozwiązywać:
11x − 7y = 13 …(I)
x − 7y = 3 …(ii)  

Metoda:

1. Wyeliminuj jedną z niewiadomych ( wyeliminujmy y) .
2. Rozwiąż drugą niewiadomą ( tutaj jest to x ).
3. Znajdź wartość nieznanego wyeliminowanego wcześniej ( znajdź wartość y )

Aby wyeliminować jedną z nieznanych (krok 1) można zastosować następujące metody:

• Metoda zastępcza
• Metoda dodawania lub odejmowania

Metoda zastępcza:
Rozwiążmy powyższe równania tą metodą.
Dla (I) otrzymujemy 11x − 7y = 13
−7y = 13 − 11x
\(y = \frac{(13 - 11x)}{-7} \)
Zastąp wartość y w drugim równaniu.
x − 7y = 3
\(x - 7(\frac{13 - 11x}{-7}) = 3 \)
x + 13 − 11x = 3
−10x = 3 − 13
−10x = −10
Dlatego x = 1
jako \(y = \frac{(13 - 11x)}{-7} \) , podstaw tutaj wartość x i uzyskaj wartość y
\(y = \frac{13 - (11 \times 1)}{-7}\)
\(y = \frac{13 - 11}{-7} \\ y = \frac{-2}{7}\)
Zatem x = 1 i y = −2 ∕ 7 jest wymaganym rozwiązaniem.

Metoda eliminacji:
Rozwiązywać:
2x + 3y = 10
x + y = 6

1. Spraw, aby współczynnik zmiennej w obu równaniach był taki sam (powiedzmy y), mnożąc oba równania przez liczbę.
   (2x + 3y = 10) × 1
   ( x + y = 6 ) × 3
   Oba równania mają teraz współczynnik y równy 3.
2. Dodaj lub odejmij, aby pozbyć się jednej zmiennej, a następnie rozwiąż równanie, pozostawiając tylko jedną zmienną (rozwiąż x)
   2x + 3y = 10
   3x + 3y = 18
   Odejmij drugie równanie od pierwszego równania.
   +2x + 3y =+10
   +3x + 3y = +18
   - - -
   ------------------
   −x = -8
   Dlatego x = 8
   y = 6 - x ⇒ y = 6 - 8 = -2
   Stąd x = 8, y = -2

Zadania tekstowe z równoczesnymi równaniami:

Przykład 1 : Suma cyfr pewnej liczby dwucyfrowej wynosi 13, a liczba ta jest o 2 większa niż 7-krotność cyfry jednostki. Znajdź liczby.
Niech x będzie na miejscu jedności, a y na miejscu dziesiątek.
10y + x = liczba = yx
y + x = 13
10y + x = 2 + 7x ⇒ 10y - 6x = 2
2(5y −3x) = 2 ⇒ 5y − 3x = 1 ⇒ \( y = \frac{1 + 3x}{5}\) … metodą podstawiania
y + x = 13 ⇒ \(\frac{1 + 3x}{5} + x = 13\)
1 + 3x + 5x = 13 × 5
1 + 8x = 65 ⇒ 8x = 64
x = 8, zatem y = 13 − x ⇒ y = 13 − 8 = 5
Liczba to 10 × 5 + 8 = 58 (Odpowiedź)

Przykład 2: Koszt 3 puszek po kawie i 2 torebek herbaty to 15 zł, a jednej puszki po kawie i 4 torebek herbaty tego samego typu to 12 zł. Znajdź koszt każdego z nich.
Niech koszt jednej puszki po kawie wynosi x $, a paczki herbaty y $.
3x + 2y = 16
1x + 4y = 12
Użyj metody eliminacji,
12x + 8y = 64
+2x + 8y = 24
- - -
----------------
10x = 40
x = 4, zatem 4 + 4y = 12 ⇒ y = 2
Koszt jednej puszki po kawie wynosi 4 zł, a jednej paczki herbaty 2 zł. (Odpowiedź)