Back to the topics list

equações lineares

Uma equação linear é uma equação para uma linha reta. Exemplo: 2x + y = 5 é uma equação linear

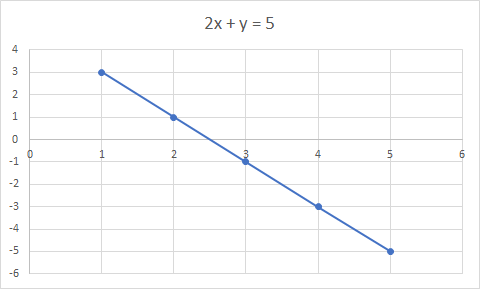
O gráfico de 2x + y = 5 é uma reta

Podemos definir uma equação linear como:

A equação linear é uma equação de grau 1 e, portanto, representa uma linha reta em um gráfico. As equações lineares também são chamadas de equações de primeiro grau , pois a maior potência da variável nessas equações é 1.

Como dizemos se uma equação é linear ou não? Vamos entender isso com alguns exemplos dados abaixo.

Exemplo:

• 2x + 3a = 5

Qualquer equação tem um grau. 2x +3y = 5 tem três termos. A maior potência da variável em uma equação é o 'grau'. Aqui é 2x, x tem uma potência 1, ou seja, x ¹ . Em 3y, y também é de potência 1, ou seja, y ¹ , portanto, esta equação é uma equação linear

• 2x + 3y + 5xy = 10

Nesta equação, o grau do termo 5xy é dois. x é de potência 1 ey é de potência 1, então o grau total, que é a soma da potência de todas as variáveis desse termo é 1 + 1 = 2. Portanto, esta equação não é uma equação linear.

• 2x + 3y + 7z + 9c = 20

Nesta equação, existem 5 termos, mas o grau de todos esses termos é 1, portanto, esta é uma equação linear.

Aqui aprendemos que para uma equação linear não há limitação de um número de variáveis na equação. A limitação está na maior potência que um termo em uma equação pode ter.

• \(\mathbf{\frac{2}{x} + y = 10}\)

Nesta equação, a potência de x é -1 (x ^-1 ), portanto esta equação não é uma equação linear.

Resolvendo Equações Lineares Simultâneas em Duas Variáveis

Um sistema de duas equações consistentes e independentes em duas variáveis é resolvido da seguinte forma:
Resolver:
11x − 7y = 13 …(eu)
x − 7y = 3 …(ii)  

Método:

1. Elimine uma das incógnitas ( vamos eliminar y) .
2. Resolva para a outra incógnita ( aqui é x ).
3. Encontre o valor da incógnita eliminada anteriormente ( encontre o valor de y )

Para eliminar um dos métodos desconhecidos (etapa 1), os seguintes podem ser usados:

• Método de substituição
• Método de adição ou subtração

Método de substituição:
Vamos resolver as equações acima usando este método.
Por (eu) obtemos 11x − 7y = 13
−7y = 13 − 11x
\(y = \frac{(13 - 11x)}{-7} \)
Substitua o valor de y na segunda equação.
x − 7y = 3
\(x - 7(\frac{13 - 11x}{-7}) = 3 \)
x + 13 − 11x = 3
−10x = 3 − 13
−10x = −10
Portanto, x = 1
como \(y = \frac{(13 - 11x)}{-7} \) , substitua o valor de x aqui e obtenha o valor de y
\(y = \frac{13 - (11 \times 1)}{-7}\)
\(y = \frac{13 - 11}{-7} \\ y = \frac{-2}{7}\)
Portanto, x = 1 e y = −2 ∕ 7 é a solução necessária.

Método de eliminação:
Resolver:
2x + 3a = 10
x + y = 6

1. Faça o coeficiente de uma variável em ambas as equações o mesmo (digamos y) multiplicando ambas as equações por um número.
   (2x + 3y = 10) × 1
   ( x + y = 6 ) × 3
   Ambas as equações agora têm um coeficiente de y como 3.
2. Adicione ou subtraia para se livrar de uma variável e, em seguida, resolva a equação com apenas uma variável restante (resolva para x)
   2x + 3a = 10
   3x + 3a = 18
   Subtraia a segunda equação da primeira equação.
   +2x + 3a = +10
   +3x + 3a = +18
   - - -
   ------------------
   −x = -8
   Portanto, x = 8
   y = 6 − x ⇒ y = 6 − 8 = −2
   Portanto x = 8, y = -2

Problemas de palavras envolvendo equações simultâneas:

Exemplo 1 : A soma dos dígitos de um determinado número de dois dígitos é 13 e o número é 2 a mais que 7 vezes o dígito da unidade. Encontre os números.
Seja x na posição da unidade e y na posição das dezenas.
10y + x = o número = yx
a + x = 13
10y + x = 2 + 7x ⇒ 10y − 6x = 2
2(5y −3x) = 2 ⇒ 5y − 3x = 1 ⇒ \( y = \frac{1 + 3x}{5}\) … usando o método de substituição
y + x = 13 ⇒ \(\frac{1 + 3x}{5} + x = 13\)
1 + 3x + 5x = 13 × 5
1 + 8x = 65 ⇒ 8x = 64
x = 8, portanto y = 13 − x ⇒ y = 13 − 8 = 5
O número é 10 × 5 + 8 = 58 (Resposta)

Exemplo 2: O custo de 3 latas de café e 2 pacotes de chá é de $ 15 e o de uma lata de café e 4 pacotes de chá do mesmo tipo é de $ 12. Descubra o custo de cada um.
Suponha que o custo de uma lata de café seja $x e de um pacote de chá seja $y.
3x + 2a = 16
1x + 4a = 12
Use o método de eliminação,
12x + 8a = 64
+2x + 8a = 24
- - -
----------------
10x = 40
x = 4, portanto 4 + 4y = 12 ⇒ y = 2
O custo de uma lata de café é de $ 4 e o custo de um pacote de chá é de $ 2. (Resposta)