Back to the topics list

линейные уравнения

Линейное уравнение — это уравнение прямой линии. Пример: 2x + y = 5 — линейное уравнение.

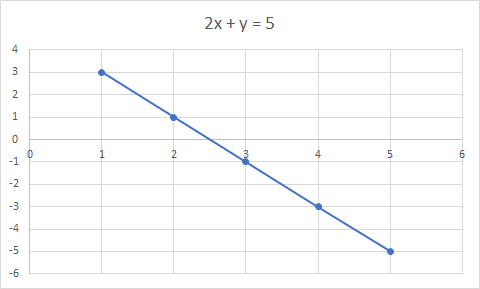
График 2x + y = 5 представляет собой прямую линию

Мы можем определить линейное уравнение как:

Линейное уравнение является уравнением степени 1 и, следовательно, представляет собой прямую линию на графике. Линейные уравнения также называют уравнениями первой степени , так как наивысшая степень переменной в этих уравнениях равна 1.

Как мы можем сказать, является ли уравнение линейным или нет? Давайте разберемся в этом на нескольких примерах, приведенных ниже.

Пример:

• 2х + 3у = 5

Любое уравнение имеет степень. 2x +3y = 5 имеет три члена. Наивысшая степень переменной в уравнении — это «степень». Здесь 2x, x имеет мощность 1, т.е. x ¹ . В 3y y также имеет степень 1, т.е. y ¹ , поэтому это уравнение является линейным уравнением

• 2x + 3y + 5xy = 10

В этом уравнении степень члена 5xy равна двум. x имеет степень 1, а y имеет степень 1, поэтому общая степень, представляющая собой сумму степеней всех переменных этого члена, равна 1 + 1 = 2. Следовательно, это уравнение не является линейным уравнением.

• 2х + 3у + 7з + 9с = 20

В этом уравнении 5 членов, но степень всех этих членов равна 1, поэтому это линейное уравнение.

Здесь мы узнали, что для линейного уравнения нет ограничений на количество переменных в уравнении. Ограничение касается наибольшей степени , которую может иметь член в уравнении.

• \(\mathbf{\frac{2}{x} + y = 10}\)

В этом уравнении степень x равна -1 (x ^-1 ), следовательно, это уравнение не является линейным уравнением.

Решение одновременных линейных уравнений с двумя переменными

Система двух непротиворечивых и независимых уравнений с двумя переменными решается следующим образом:
Решать:
11х - 7у = 13 …(я)
х - 7у = 3 …(ii)  

Метод:

1. Устраните одно из неизвестных ( давайте исключим y) .
2. Решите для другого неизвестного ( здесь это x ).
3. Найдите значение ранее исключенного неизвестного ( найдите значение y )

Для устранения одного из неизвестных (шаг 1) можно использовать следующие методы:

• Метод замены
• Метод сложения или вычитания

Метод замены:
Решим приведенные выше уравнения, используя этот метод.
За (я) мы получаем 11x - 7y = 13
−7y = 13 − 11x
\(y = \frac{(13 - 11x)}{-7} \)
Подставьте значение y во второе уравнение.
х - 7у = 3
\(x - 7(\frac{13 - 11x}{-7}) = 3 \)
х + 13 - 11х = 3
−10x = 3 − 13
−10x = −10
Следовательно, х = 1
как \(y = \frac{(13 - 11x)}{-7} \) , подставьте сюда значение x и получите значение y
\(y = \frac{13 - (11 \times 1)}{-7}\)
\(y = \frac{13 - 11}{-7} \\ y = \frac{-2}{7}\)
Следовательно, x = 1 и y = −2 ∕ 7 — искомое решение.

Метод устранения:
Решать:
2х + 3у = 10
х + у = 6

1. Сделайте коэффициент переменной в обоих уравнениях одинаковым (скажем, у), умножив оба уравнения на число.
   (2x + 3y = 10) × 1
   ( х + у = 6 ) × 3
   Теперь оба уравнения имеют коэффициент y, равный 3.
2. Добавьте или вычтите, чтобы избавиться от одной переменной, а затем решите уравнение только с одной оставшейся переменной (решите для x)
   2х + 3у = 10
   3х + 3у = 18
   Вычесть второе уравнение из первого уравнения.
   +2x + 3y =+10
   +3x + 3y = +18
   - - -
   ------------------
   −х = -8
   Следовательно, х = 8
   у = 6 - х ⇒ у = 6 - 8 = -2
   Следовательно , х = 8, у = -2

Словесные задачи с одновременными уравнениями:

Пример 1 : Сумма цифр некоторого двузначного числа равна 13, и это число в 2 раза больше, чем в 7 раз превышает разряд единицы. Найдите числа.
Пусть х стоит на месте единиц, а у на месте десятков.
10у + х = число=ух
у + х = 13
10у + х = 2 + 7х ⇒ 10у - 6х = 2
2(5y −3x) = 2 ⇒ 5y − 3x = 1 ⇒ \( y = \frac{1 + 3x}{5}\) … используя метод подстановки
у + х = 13 ⇒ \(\frac{1 + 3x}{5} + x = 13\)
1 + 3х + 5х = 13 × 5
1 + 8х = 65 ⇒ 8х = 64.
х = 8, поэтому у = 13 - х ⇒ у = 13 - 8 = 5
Число 10 × 5 + 8 = 58 (Ответ)

Пример 2: Стоимость 3 банок кофе и 2 пакетиков чая составляет 15 долларов США, а стоимость одной банки кофе и 4 пакетов чая того же типа — 12 долларов США. Найдите стоимость каждого.
Пусть стоимость одной банки кофе $x, а одной пачки чая $y.
3х + 2у = 16
1х + 4у = 12
Используйте метод исключения,
12х + 8у = 64
+2x + 8y = 24
- - -
----------------
10х = 40
х = 4, поэтому 4 + 4у = 12 ⇒ у = 2
Стоимость одной банки кофе — 4 доллара, а стоимость одного пакетика чая — 2 доллара. (Ответ)