Back to the topics list

linjära ekvationer

En linjär ekvation är en ekvation för en rät linje. Exempel: 2x + y = 5 är en linjär ekvation

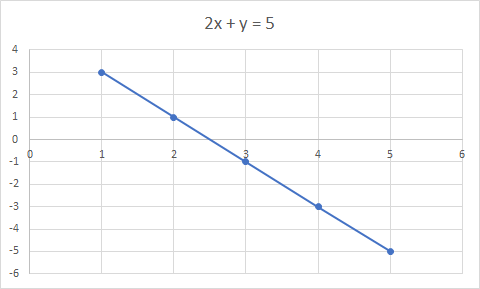
Grafen för 2x + y = 5 är en rät linje

Vi kan definiera en linjär ekvation som:

Linjär ekvation är en ekvation av grad 1 och representerar därför en rät linje på en graf. Linjära ekvationer kallas också förstagradsekvationer , eftersom den högsta potensen av variabeln i dessa ekvationer är 1.

Hur säger vi om en ekvation är linjär eller inte? Låt oss förstå detta med några exempel nedan.

Exempel:

• 2x + 3y = 5

Varje ekvation har en grad. 2x +3y = 5 har tre termer. Den högsta potensen av variabeln i en ekvation är "graden". Här är 2x, x har en potens 1 dvs x ¹ . I 3y är y också av potens 1 dvs y ¹ , därför är denna ekvation en linjär ekvation

• 2x + 3y + 5xy = 10

I denna ekvation är graden av termen 5xy två. x är av potens 1, och y är av potens 1, så den totala graden, som är summan av potensen av alla variabler i den termen, är 1 + 1 = 2. Därför är denna ekvation inte en linjär ekvation.

• 2x + 3y + 7z + 9c = 20

I denna ekvation finns det 5 termer men graden av alla dessa termer är 1, därför är detta en linjär ekvation.

Här lärde vi oss att för en linjär ekvation finns det ingen begränsning på ett antal variabler i ekvationen. Begränsningen ligger på den högsta makt som en term i en ekvation kan ha.

• \(\mathbf{\frac{2}{x} + y = 10}\)

I denna ekvation är potensen av x -1 (x ^-1 ), därför är denna ekvation inte en linjär ekvation.

Lösa simultana linjära ekvationer i två variabler

Ett system med två konsekventa och oberoende ekvationer i två variabler löses enligt följande:
Lösa:
11x − 7y = 13 …(i)
x − 7y = 3 …(ii)  

Metod:

1. Eliminera en av de okända ( låt oss eliminera y) .
2. Lös för det andra okända ( här är det x ).
3. Hitta värdet på det okända som tidigare eliminerats ( hitta värdet på y)

För att eliminera en av de okända (steg 1) kan följande metoder användas:

• Substitutionsmetod
• Additions- eller subtraktionsmetod

Ersättningsmetod:
Låt oss lösa ovanstående ekvationer med denna metod.
För (i) vi får 11x − 7y = 13
−7y = 13 − 11x
\(y = \frac{(13 - 11x)}{-7} \)
Ersätt värdet på y i andra ekvationen.
x − 7y = 3
\(x - 7(\frac{13 - 11x}{-7}) = 3 \)
x + 13 − 11x = 3
−10x = 3 − 13
−10x =−10
Därför är x = 1
som \(y = \frac{(13 - 11x)}{-7} \) ersätt värdet på x här och få värdet på y
\(y = \frac{13 - (11 \times 1)}{-7}\)
\(y = \frac{13 - 11}{-7} \\ y = \frac{-2}{7}\)
Därför är x = 1 och y = −2 ∕ 7 den nödvändiga lösningen.

Elimineringsmetod:
Lösa:
2x + 3y = 10
x + y = 6

1. Gör koefficienten för en variabel i båda ekvationerna lika (låt oss säga y) genom att multiplicera båda ekvationerna med ett tal.
   (2x + 3y = 10) × 1
   ( x + y = 6 ) × 3
   Båda ekvationerna har nu koefficienten y som 3.
2. Addera eller subtrahera för att bli av med en variabel och lös sedan ekvationen med bara en variabel kvar (lös för x)
   2x + 3y = 10
   3x + 3y = 18
   Subtrahera den andra ekvationen från den första ekvationen.
   +2x + 3y =+10
   +3x + 3y = +18
   -- -
   ------------------
   −x = -8
   Därför är x = 8
   y = 6 − x ⇒ y = 6 − 8 = −2
   Följaktligen är x = 8, y = -2

Ordproblem som involverar samtidiga ekvationer:

Exempel 1 : Summan av siffrorna i ett visst tvåsiffrigt tal är 13 och talet är 2 mer än 7 gånger enhetens siffra. Hitta siffrorna.
Låt x vara på enhetsplatsen och y på tiotalsplatsen.
10y + x = talet=yx
y + x = 13
10y + x = 2 + 7x ⇒ 10y − 6x = 2
2(5y −3x) = 2 ⇒ 5y − 3x = 1 ⇒ \( y = \frac{1 + 3x}{5}\) … med substitutionsmetod
y + x = 13 ⇒ \(\frac{1 + 3x}{5} + x = 13\)
1 + 3x + 5x = 13 × 5
1 + 8x = 65 ⇒ 8x = 64
x = 8, därför y = 13 − x ⇒ y = 13 − 8 = 5
Siffran är 10 × 5 + 8 = 58 (Svar)

Exempel 2: Kostnaden för 3 kaffeburkar och 2 tepaket är $15 och kostnaden för en kaffeburk och 4 tepaket av samma typ är $12. Hitta kostnaden för varje.
Låt kostnaden för en kaffeburk vara $x och för ett tepaket är $y.
3x + 2y = 16
1x + 4y = 12
Använd elimineringsmetoden,
12x + 8y = 64
+2x + 8y = 24
-- -
----------------
10x = 40
x = 4, därför 4 + 4y = 12 ⇒ y = 2
Kostnaden för en kaffeburk är $4 och kostnaden för ett tepaket är $2.(Svar)