Back to the topics list

สมการเชิงเส้น

สมการเชิงเส้น คือสมการของเส้นตรง ตัวอย่าง: 2x + y = 5 เป็นสมการเชิงเส้น

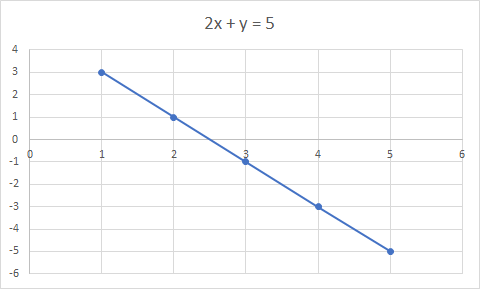
กราฟของ 2x + y = 5 เป็นเส้นตรง

เราสามารถกำหนด สมการเชิงเส้น ได้ดังนี้

สมการเชิงเส้นคือสมการของดีกรี 1 และด้วยเหตุนี้จึงแทนเส้นตรงบนกราฟ สมการเชิงเส้น เรียกอีกอย่างว่า สมการดีกรีที่หนึ่ง เนื่องจากกำลังสูงสุดของตัวแปรในสมการเหล่านี้คือ 1

เราจะบอกได้อย่างไรว่าสมการเป็นเชิงเส้นหรือไม่? มาทำความเข้าใจกับตัวอย่างต่อไปนี้

ตัวอย่าง:

• 2x + 3y = 5

สมการใดๆ มีดีกรี 2x +3y = 5 มีสามพจน์ กำลังสูงสุดของตัวแปรในสมการคือ 'ดีกรี' นี่คือ 2x, x มีกำลัง 1 คือ x ¹ ใน 3y, y มีกำลัง 1 เช่น y ¹ ดังนั้นสมการนี้จึงเป็นสมการเชิงเส้น

• 2x + 3y + 5xy = 10

ในสมการนี้ ดีกรีของเทอม 5xy คือ 2 x กำลัง 1 และ y กำลัง 1 ดังนั้นดีกรีรวม ซึ่งเป็นผลบวกของกำลังของตัวแปรทั้งหมดของเทอมนั้นคือ 1 + 1 = 2 ดังนั้น สมการนี้จึง ไม่ใช่ สมการเชิงเส้น

• 2x + 3y + 7z + 9c = 20

ในสมการนี้มี 5 พจน์ แต่ดีกรีของพจน์ทั้งหมดคือ 1 ดังนั้นนี่คือสมการเชิงเส้น

ที่นี่เราได้เรียนรู้ว่าสำหรับสมการเชิงเส้น ไม่มีการจำกัดจำนวนตัวแปรในสมการ ข้อจำกัดอยู่ที่ พลังสูงสุด ที่พจน์ในสมการสามารถมีได้

• \(\mathbf{\frac{2}{x} + y = 10}\)

ในสมการนี้ กำลังของ x คือ -1 (x ^-1 ) ดังนั้นสมการนี้จึง ไม่ใช่ สมการเชิงเส้น

การแก้สมการเชิงเส้นพร้อมกันในสองตัวแปร

ระบบของสมการสองสมการที่สอดคล้องกันและเป็นอิสระต่อกันในตัวแปรสองตัวได้รับการแก้ไขดังนี้:
แก้ปัญหา:
11x − 7y = 13 …(ฉัน)
x − 7y = 3 …(ii)  

วิธี:

1. กำจัดหนึ่งในสิ่งที่ไม่รู้จัก ( มากำจัด y) กันเถอะ
2. แก้ปัญหาสำหรับสิ่งที่ไม่รู้จักอื่น ๆ ( นี่คือ x )
3. ค้นหาค่าของสิ่งที่ไม่รู้จักที่ถูกกำจัดไปก่อนหน้านี้ ( ค้นหาค่าของ y )

หากต้องการกำจัดวิธีใดวิธีหนึ่งที่ไม่รู้จัก (ขั้นตอนที่ 1) ต่อไปนี้สามารถใช้ได้:

• วิธีการทดแทน
• วิธีบวกหรือลบ

วิธีการทดแทน:
ให้เราแก้สมการข้างต้นโดยใช้วิธีนี้
สำหรับ (ฉัน) เราได้ 11x − 7y = 13
−7y = 13 − 11x
\(y = \frac{(13 - 11x)}{-7} \)
แทนค่า y ในสมการที่สอง
x − 7y = 3
\(x - 7(\frac{13 - 11x}{-7}) = 3 \)
x + 13 − 11x = 3
−10x = 3 − 13
−10x = −10
ดังนั้น x = 1
เช่น \(y = \frac{(13 - 11x)}{-7} \) แทนค่า x ที่นี่และรับค่าของ y
\(y = \frac{13 - (11 \times 1)}{-7}\)
\(y = \frac{13 - 11}{-7} \\ y = \frac{-2}{7}\)
ดังนั้น x = 1 และ y = −2 ∕ 7 จึงเป็นคำตอบที่ต้องการ

วิธีการกำจัด:
แก้ปัญหา:
2x + 3y = 10
x + y = 6

1. ทำให้ค่าสัมประสิทธิ์ของตัวแปรในสมการทั้งสองเท่ากัน (สมมุติว่า y) โดยการคูณสมการทั้งสองด้วยตัวเลข
   (2x + 3y = 10) × 1
   ( x + y = 6 ) × 3
   สมการทั้งสองตอนนี้มีค่าสัมประสิทธิ์ของ y เป็น 3
2. บวกหรือลบเพื่อกำจัดตัวแปรหนึ่งตัวแล้วแก้สมการโดยเหลือตัวแปรเดียว (แก้หา x)
   2x + 3y = 10
   3x + 3y = 18
   ลบสมการที่สองออกจากสมการแรก
   +2x + 3y = +10
   +3x + 3y = +18
   - - -
   ------------------
   −x = -8
   ดังนั้น x = 8
   y = 6 − x ⇒ y = 6 − 8 = −2
   ดังนั้น x = 8, y = -2

ปัญหาคำศัพท์ที่เกี่ยวข้องกับสมการพร้อมกัน:

ตัวอย่างที่ 1 ผลบวกของเลขสองหลักจำนวนหนึ่งคือ 13 และเลขนั้นเป็น 2 มากกว่า 7 เท่าของหลักหน่วย ค้นหาตัวเลข
ให้ x อยู่ที่หลักหน่วย และ y อยู่ที่หลักสิบ
10y + x = จำนวน = yx
y + x = 13
10y + x = 2 + 7x ⇒ 10y − 6x = 2
2(5y −3x) = 2 ⇒ 5y − 3x = 1 ⇒ \( y = \frac{1 + 3x}{5}\) … โดยใช้วิธีแทนที่
y + x = 13 ⇒ \(\frac{1 + 3x}{5} + x = 13\)
1 + 3x + 5x = 13 × 5
1 + 8x = 65 ⇒ 8x = 64
x = 8 ดังนั้น y = 13 − x ⇒ y = 13 − 8 = 5
จำนวนคือ 10 × 5 + 8 = 58 (คำตอบ)

ตัวอย่างที่ 2: ราคาของกาแฟ 3 กระป๋องและชา 2 ซองคือ 15 ดอลลาร์ และราคาของกาแฟ 1 กระป๋องและชา 4 ซองในประเภทเดียวกันคือ 12 ดอลลาร์ ค้นหาค่าใช้จ่ายของแต่ละ
ให้ราคาของกระป๋องกาแฟหนึ่งกระป๋องเท่ากับ $x และสำหรับหนึ่งซองคือ $y
3x + 2y = 16
1x + 4y = 12
ใช้วิธีกำจัด
12x + 8y = 64
+2x + 8y = 24
- - -
----------------
10x = 40
x = 4 ดังนั้น 4 + 4y = 12 ⇒ y = 2
ราคาของกระป๋องกาแฟหนึ่งกระป๋องคือ $4 และราคาของชาหนึ่งซองคือ $2 (คำตอบ)