Back to the topics list

linear na equation

Ang Linear Equation ay isang equation para sa isang tuwid na linya. Halimbawa: 2x + y = 5 ay isang linear equation

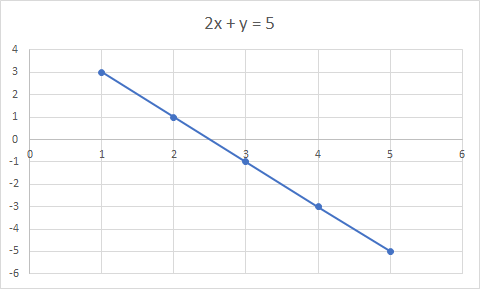
Ang graph ng 2x + y = 5 ay isang tuwid na linya

Maaari naming tukuyin ang isang Linear Equation bilang:

Ang Linear Equation ay isang Equation ng degree 1 at samakatuwid ay kumakatawan sa isang tuwid na linya sa isang graph. Ang mga Linear Equation ay tinatawag ding mga first degree equation , dahil ang pinakamataas na kapangyarihan ng variable sa mga equation na ito ay 1.

Paano natin masasabi kung ang isang equation ay linear o hindi? Unawain natin ito sa ilang mga halimbawang ibinigay sa ibaba.

Halimbawa:

• 2x + 3y = 5

Ang anumang equation ay may degree. Ang 2x +3y = 5 ay may tatlong termino. Ang pinakamataas na kapangyarihan ng variable sa isang equation ay ang 'degree'. Narito ang 2x, ang x ay may kapangyarihan 1 ie x ¹ . Sa 3y, y din ay may kapangyarihan 1 ie y ¹ , samakatuwid ang equation na ito ay isang linear equation

• 2x + 3y + 5xy = 10

Sa equation na ito, ang antas ng terminong 5xy ay dalawa. x ay ng kapangyarihan 1, at y ay ng kapangyarihan 1 kaya ang kabuuang antas, na kung saan ay ang kabuuan ng kapangyarihan ng lahat ng mga variable ng term na iyon ay 1 + 1 = 2. Samakatuwid, ang equation na ito ay hindi isang linear equation.

• 2x + 3y + 7z + 9c = 20

Sa equation na ito, mayroong 5 termino ngunit ang antas ng lahat ng terminong ito ay 1, samakatuwid ito ay isang linear equation.

Dito namin natutunan na para sa isang Linear Equation ay walang limitasyon sa isang bilang ng mga variable sa equation. Ang limitasyon ay nasa pinakamataas na kapangyarihan na maaaring magkaroon ng isang termino sa isang equation.

• \(\mathbf{\frac{2}{x} + y = 10}\)

Sa equation na ito, ang kapangyarihan ng x ay -1 (x ^-1 ), kaya ang equation na ito ay hindi isang linear equation.

Paglutas ng Sabay-sabay na Linear Equation sa Dalawang Variable

Ang isang sistema ng dalawang pare-pareho at independiyenteng mga equation sa dalawang variable ay malulutas bilang mga sumusunod:
Lutasin:
11x − 7y = 13 …(i)
x − 7y = 3 …(ii)  

Paraan:

1. Tanggalin ang isa sa mga hindi alam( tanggalin natin ang y) .
2. Lutasin ang iba pang hindi alam ( narito ito x ).
3. Hanapin ang halaga ng hindi kilalang inalis dati ( hanapin ang halaga ng y )

Upang alisin ang isa sa mga hindi alam (hakbang 1) ang mga sumusunod na pamamaraan ay maaaring gamitin:

• Pamamaraan ng pagpapalit
• Paraan ng Pagdaragdag o Pagbabawas

Paraan ng pagpapalit:
Lutasin natin ang mga equation sa itaas gamit ang pamamaraang ito.
Para sa (i) nakukuha natin ang 11x − 7y = 13
−7y = 13 − 11x
\(y = \frac{(13 - 11x)}{-7} \)
Palitan ang halaga ng y sa pangalawang equation.
x − 7y = 3
\(x - 7(\frac{13 - 11x}{-7}) = 3 \)
x + 13 − 11x = 3
−10x = 3 − 13
−10x =−10
Samakatuwid, x = 1
bilang \(y = \frac{(13 - 11x)}{-7} \) , palitan ang halaga ng x dito at kunin ang halaga ng y
\(y = \frac{13 - (11 \times 1)}{-7}\)
\(y = \frac{13 - 11}{-7} \\ y = \frac{-2}{7}\)
Kaya, x = 1 at y = −2 ∕ 7 ang kinakailangang solusyon.

Paraan ng pag-aalis:
Lutasin:
2x + 3y = 10
x + y = 6

1. Gawing magkapareho ang koepisyent ng isang variable sa parehong mga equation(sabihin natin y) sa pamamagitan ng pag-multiply ng parehong equation sa isang numero.
   (2x + 3y = 10) × 1
   ( x + y = 6 ) × 3
   Ang parehong mga equation ay mayroon na ngayong coefficient ng y bilang 3.
2. Magdagdag o ibawas upang maalis ang isang variable at pagkatapos ay lutasin ang equation na may isang variable na lang ang natitira (solve para sa x)
   2x + 3y = 10
   3x + 3y = 18
   Ibawas ang pangalawang equation mula sa unang equation.
   +2x + 3y =+10
   +3x + 3y = +18
   ---
   -------------------
   −x = -8
   Samakatuwid, x = 8
   y = 6 − x ⇒ y = 6 − 8 = −2
   Samakatuwid x = 8, y = -2

Mga Problema sa Salita na kinasasangkutan ng sabay-sabay na mga equation:

Halimbawa 1 : Ang kabuuan ng mga digit ng isang tiyak na dalawang-digit na numero ay 13 at ang numero ay 2 higit sa 7 beses sa digit ng yunit. Hanapin ang mga numero.
Hayaan ang x ay nasa unit place at y sa tens place.
10y + x = ang numero=yx
y + x = 13
10y + x = 2 + 7x ⇒ 10y − 6x = 2
2(5y −3x) = 2 ⇒ 5y − 3x = 1 ⇒ \( y = \frac{1 + 3x}{5}\) … gamit ang paraan ng pagpapalit
y + x = 13 ⇒ \(\frac{1 + 3x}{5} + x = 13\)
1 + 3x + 5x = 13 × 5
1 + 8x = 65 ⇒ 8x = 64
x = 8, samakatuwid y = 13 − x ⇒ y = 13 − 8 = 5
Ang numero ay 10 × 5 + 8 = 58 (Sagot)

Halimbawa 2: Ang halaga ng 3 lata ng kape at 2 pakete ng tsaa ay $15 at ang halaga ng isang lata ng kape at 4 na pakete ng tsaa ng parehong uri ay $12. Hanapin ang halaga ng bawat isa.
Hayaang ang halaga ng isang lata ng kape ay $x at para sa isang pakete ng tsaa ay $y.
3x + 2y = 16
1x + 4y = 12
Gamitin ang paraan ng pag-aalis,
12x + 8y = 64
+2x + 8y = 24
---
----------------
10x = 40
x = 4, samakatuwid 4 + 4y = 12 ⇒ y = 2
Ang halaga ng isang lata ng kape ay $4 at ang halaga ng isang pakete ng tsaa ay $2.(Sagot)