Back to the topics list

лінійні рівняння

Лінійне рівняння – це рівняння для прямої лінії. Приклад: 2x + y = 5 — лінійне рівняння

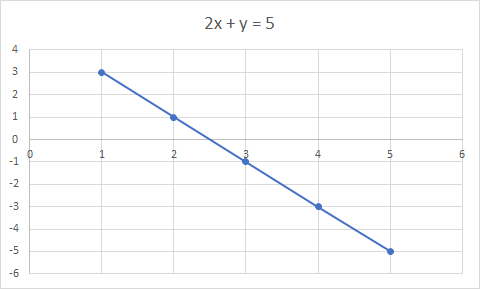
Графік 2x + y = 5 є прямою лінією

Ми можемо визначити лінійне рівняння як:

Лінійне рівняння є рівнянням ступеня 1 і, отже, представляє пряму лінію на графіку. Лінійні рівняння також називаються рівняннями першого ступеня , оскільки найвищий ступінь змінної в цих рівняннях дорівнює 1.

Як сказати, чи є рівняння лінійним чи ні? Давайте зрозуміємо це на кількох прикладах, наведених нижче.

приклад:

• 2x + 3y = 5

Будь-яке рівняння має степінь. 2x +3y = 5 має три члени. Найвищий ступінь змінної в рівнянні є «ступенем». Ось 2x, x має ступінь 1, тобто x ¹ . У 3y y також має ступінь 1, тобто y ¹ , тому це рівняння є лінійним рівнянням

• 2x + 3y + 5xy = 10

У цьому рівнянні ступінь члена 5xy дорівнює двом. x має ступінь 1, а y має ступінь 1, тому загальний ступінь, який є сумою степенів усіх змінних цього члена, дорівнює 1 + 1 = 2. Отже, це рівняння не є лінійним рівнянням.

• 2x + 3y + 7z + 9c = 20

У цьому рівнянні є 5 членів, але степінь усіх цих членів дорівнює 1, тому це лінійне рівняння.

Тут ми дізналися, що для лінійного рівняння немає обмежень на кількість змінних у рівнянні. Обмеження стосується найвищого ступеня , який може мати член у рівнянні.

• \(\mathbf{\frac{2}{x} + y = 10}\)

У цьому рівнянні ступінь x дорівнює -1 (x ^-1 ), тому це рівняння не є лінійним.

Розв’язування одночасних лінійних рівнянь із двома змінними

Система двох узгоджених і незалежних рівнянь з двома змінними розв’язується наступним чином:
Розв'язати:
11x − 7y = 13 …(i)
x − 7y = 3 …(ii)  

Метод:

1. Виключіть одне з невідомих ( вилучимо y) .
2. Знайдіть інше невідоме ( тут це x ).
3. Знайти значення невідомого, вилученого раніше ( знайти значення y )

Для усунення одного з невідомих (крок 1) можна використати такі методи:

• Метод підстановки
• Спосіб додавання або віднімання

Спосіб заміни:
Розв’яжемо наведені вище рівняння цим методом.
для (і) отримуємо 11x − 7y = 13
−7y = 13 − 11x
\(y = \frac{(13 - 11x)}{-7} \)
Підставте значення y у друге рівняння.
x − 7y = 3
\(x - 7(\frac{13 - 11x}{-7}) = 3 \)
x + 13 − 11x = 3
−10x = 3 − 13
−10x =−10
Отже, x = 1
як \(y = \frac{(13 - 11x)}{-7} \) , підставте сюди значення x і отримайте значення y
\(y = \frac{13 - (11 \times 1)}{-7}\)
\(y = \frac{13 - 11}{-7} \\ y = \frac{-2}{7}\)
Отже, x = 1 і y = −2 ∕ 7 є шуканим розв’язком.

Спосіб усунення:
Розв'язати:
2x + 3y = 10
x + y = 6

1. Зробіть коефіцієнт змінної в обох рівняннях однаковим (скажімо, y), помноживши обидва рівняння на число.
   (2x + 3y = 10) × 1
   ( x + y = 6 ) × 3
   Тепер обидва рівняння мають коефіцієнт y як 3.
2. Додайте або відніміть, щоб позбутися однієї змінної, а потім розв’яжіть рівняння лише з однією змінною (розв’яжіть для x)
   2x + 3y = 10
   3x + 3y = 18
   Відніміть друге рівняння від першого рівняння.
   +2x + 3y =+10
   +3x + 3y = +18
   - - -
   ------------------
   −x = -8
   Тому х = 8
   y = 6 − x ⇒ y = 6 − 8 = −2
   Отже, x = 8, y = -2

Текстові задачі з одночасними рівняннями:

Приклад 1 : сума цифр певного двоцифрового числа дорівнює 13, а це число на 2 більше, ніж цифра одиниці в 7 разів. Знайди числа.
Нехай x стоїть у розряді одиниць, а y — у розряді десятків.
10y + x = число=yx
y + x = 13
10y + x = 2 + 7x ⇒ 10y − 6x = 2
2(5y −3x) = 2 ⇒ 5y − 3x = 1 ⇒ \( y = \frac{1 + 3x}{5}\) … з використанням методу підстановки
y + x = 13 ⇒ \(\frac{1 + 3x}{5} + x = 13\)
1 + 3x + 5x = 13 × 5
1 + 8x = 65 ⇒ 8x = 64
x = 8, тому y = 13 − x ⇒ y = 13 − 8 = 5
Число 10 × 5 + 8 = 58 (відповідь)

Приклад 2: вартість 3 банок кави та 2 пакетів чаю становить 15 доларів, а вартість однієї банки кави та 4 пакетів чаю того ж типу – 12 доларів. Знайти вартість кожного.
Нехай вартість однієї банки кави дорівнює x $, а однієї пачки чаю — $y.
3x + 2y = 16
1x + 4y = 12
Використовуйте метод елімінації,
12x + 8y = 64
+2x + 8y = 24
- - -
----------------
10x = 40
x = 4, тому 4 + 4y = 12 ⇒ y = 2
Вартість однієї банки кави – 4 долари, а пакетика чаю – 2 долари. (Відповідь)