Back to the topics list

لکیری مساوات

ایک لکیری مساوات ایک سیدھی لکیر کے لیے ایک مساوات ہے۔ مثال: 2x + y = 5 ایک لکیری مساوات ہے۔

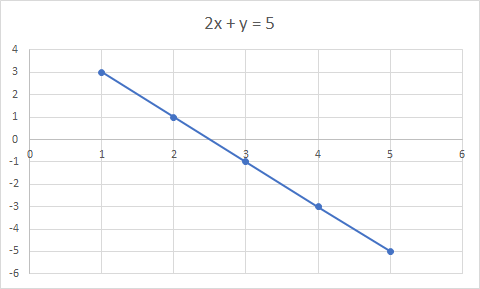
2x + y = 5 کا گراف ایک سیدھی لکیر ہے۔

ہم ایک لکیری مساوات کی تعریف اس طرح کر سکتے ہیں:

لکیری مساوات ڈگری 1 کی مساوات ہے اور اس وجہ سے گراف پر سیدھی لکیر کی نمائندگی کرتی ہے۔ لکیری مساوات کو پہلی ڈگری کی مساوات بھی کہا جاتا ہے، کیونکہ ان مساوات میں متغیر کی سب سے زیادہ طاقت 1 ہے۔

ہم کیسے کہہ سکتے ہیں کہ مساوات لکیری ہے یا نہیں؟ آئیے ذیل میں دی گئی چند مثالوں سے اس کو سمجھتے ہیں۔

مثال:

• 2x + 3y = 5

کسی بھی مساوات کی ڈگری ہوتی ہے۔ 2x +3y = 5 میں تین اصطلاحات ہیں۔ ایک مساوات میں متغیر کی سب سے زیادہ طاقت 'ڈگری' ہے۔ یہاں 2x ہے، x کی طاقت 1 ہے یعنی x ¹ ۔ 3y میں، y بھی طاقت 1 کا ہے یعنی y ¹ ، لہذا یہ مساوات ایک لکیری مساوات ہے

• 2x + 3y + 5xy = 10

اس مساوات میں، اصطلاح 5xy کی ڈگری دو ہے۔ x طاقت 1 کا ہے، اور y طاقت 1 کا ہے لہذا کل ڈگری، جو کہ اس اصطلاح کے تمام متغیرات کی طاقت کا خلاصہ ہے 1 + 1 = 2۔ لہذا، یہ مساوات لکیری مساوات نہیں ہے۔

• 2x + 3y + 7z + 9c = 20

اس مساوات میں، 5 اصطلاحات ہیں لیکن ان تمام شرائط کی ڈگری 1 ہے، لہذا یہ ایک لکیری مساوات ہے۔

یہاں ہم نے سیکھا کہ لکیری مساوات کے لیے مساوات میں متعدد متغیرات پر کوئی پابندی نہیں ہے۔ حد سب سے زیادہ طاقت پر ہے جو ایک مساوات میں ایک اصطلاح میں ہوسکتی ہے۔

• \(\mathbf{\frac{2}{x} + y = 10}\)

اس مساوات میں، x کی طاقت -1 (x ^-1 ) ہے، اس لیے یہ مساوات لکیری مساوات نہیں ہے۔

دو متغیرات میں بیک وقت لکیری مساوات کو حل کرنا

دو متغیرات میں دو مستقل اور آزاد مساوات کا نظام مندرجہ ذیل حل کیا جاتا ہے:
حل:
11x − 7y = 13 …(میں)
x − 7y = 3 …(ii)  

طریقہ:

1. نامعلوم میں سے ایک کو ختم کریں ( آئیے ختم کریں y) ۔
2. دوسرے نامعلوم کے لیے حل کریں ( یہاں یہ ہے x )۔
3. پہلے ختم شدہ نامعلوم کی قدر تلاش کریں ( y کی قدر تلاش کریں )

کسی نامعلوم (مرحلہ 1) کو ختم کرنے کے لیے درج ذیل طریقے استعمال کیے جا سکتے ہیں:

• متبادل طریقہ
• اضافے یا گھٹانے کا طریقہ

متبادل طریقہ:
آئیے اس طریقہ کو استعمال کرتے ہوئے مندرجہ بالا مساوات کو حل کریں۔
کے لیے (میں) ہمیں 11x −7y = 13 ملتا ہے۔
−7y = 13 − 11x
\(y = \frac{(13 - 11x)}{-7} \)
دوسری مساوات میں y کا متبادل قدر۔
x − 7y = 3
\(x - 7(\frac{13 - 11x}{-7}) = 3 \)
x + 13 − 11x = 3
−10x = 3 − 13
−10x =−10
لہذا، x = 1
جیسا کہ \(y = \frac{(13 - 11x)}{-7} \) ، یہاں x کی قدر کو تبدیل کریں اور y کی قدر حاصل کریں
\(y = \frac{13 - (11 \times 1)}{-7}\)
\(y = \frac{13 - 11}{-7} \\ y = \frac{-2}{7}\)
لہذا، x = 1 اور y = −2 ∕ 7 مطلوبہ حل ہے۔

خاتمے کا طریقہ:
حل:
2x + 3y = 10
x + y = 6

1. دونوں مساواتوں میں متغیر کے عدد کو یکساں بنائیں (آئیے کہتے ہیں y) دونوں مساوات کو عدد سے ضرب دے کر۔
   (2x + 3y = 10) × 1
   ( x + y = 6 ) × 3
   دونوں مساوات میں اب y کا عدد 3 ہے۔
2. ایک متغیر سے چھٹکارا حاصل کرنے کے لیے جوڑیں یا گھٹائیں اور پھر صرف ایک متغیر کے ساتھ مساوات کو حل کریں (x کے لیے حل کریں)
   2x + 3y = 10
   3x + 3y = 18
   پہلی مساوات سے دوسری مساوات کو گھٹائیں۔
   +2x + 3y =+10
   +3x + 3y = +18
   - - -
   ----------------------------------
   −x = -8
   لہذا، x = 8
   y = 6 − x ⇒ y = 6 − 8 = −2
   اس لیے x = 8، y = -2

الفاظ کے مسائل جن میں بیک وقت مساوات شامل ہیں:

مثال 1 : ایک مخصوص دو ہندسوں کے ہندسوں کا مجموعہ 13 ہے اور نمبر یونٹ کے ہندسے سے 7 گنا زیادہ ہے۔ نمبر تلاش کریں۔
آئیے x کو اکائی کی جگہ پر اور y کو دسیوں کی جگہ پر۔
10y + x = نمبر = yx
y + x = 13
10y + x = 2 + 7x ⇒ 10y − 6x = 2
2(5y −3x) = 2 ⇒ 5y − 3x = 1 ⇒ \( y = \frac{1 + 3x}{5}\) … متبادل طریقہ استعمال کرتے ہوئے
y + x = 13 ⇒ \(\frac{1 + 3x}{5} + x = 13\)
1 + 3x + 5x = 13 × 5
1 + 8x = 65 ⇒ 8x = 64
x = 8، لہذا y = 13 − x ⇒ y = 13 − 8 = 5
نمبر ہے 10 × 5 + 8 = 58 (جواب)

مثال 2: 3 کافی ٹن اور 2 چائے کے پیکٹ کی قیمت $15 ہے اور ایک کافی ٹن اور اسی قسم کے 4 چائے کے پیکٹوں کی قیمت $12 ہے۔ ہر ایک کی قیمت معلوم کریں۔
ایک کافی ٹن کی قیمت $x ہے اور ایک چائے کے پیکٹ کی قیمت $y ہے۔
3x + 2y = 16
1x + 4y = 12
خاتمے کا طریقہ استعمال کریں،
12x + 8y = 64
+2x + 8y = 24
- - -
----------------
10x = 40
x = 4، لہذا 4 + 4y = 12 ⇒ y = 2
ایک کافی ٹن کی قیمت $4 ہے اور ایک چائے کے پیکٹ کی قیمت $2 ہے۔ (جواب)