Back to the topics list

chiziqli tenglamalar

Chiziqli tenglama to'g'ri chiziq uchun tenglamadir. Misol: 2x + y = 5 chiziqli tenglama

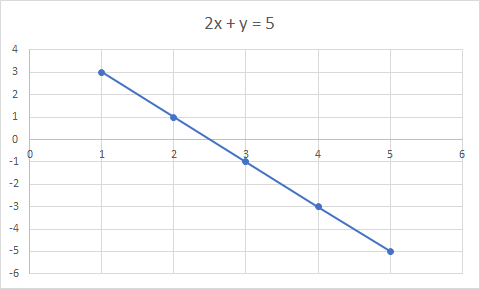
2x + y = 5 ning grafigi to'g'ri chiziqdir

Biz chiziqli tenglamani quyidagicha belgilashimiz mumkin:

Chiziqli tenglama 1-darajali tenglama bo'lib, grafikdagi to'g'ri chiziqni ifodalaydi. Chiziqli tenglamalar birinchi darajali tenglamalar deb ham ataladi, chunki bu tenglamalardagi o'zgaruvchining eng yuqori kuchi 1 ga teng.

Tenglama chiziqli yoki chiziqli emasligini qanday aytamiz? Keling, buni quyida keltirilgan bir nechta misollar bilan tushunaylik.

Misol:

• 2x + 3y = 5

Har qanday tenglama darajaga ega. 2x +3y = 5 uchta haddan iborat. Tenglamadagi o'zgaruvchining eng yuqori kuchi "daraja" dir. Bu erda 2x, x 1 kuchga ega, ya'ni x ¹ . 3y da y ham 1 ya'ni y ¹ quvvatga ega, shuning uchun bu tenglama chiziqli tenglamadir.

• 2x + 3y + 5xy = 10

Bu tenglamada 5xy atamasining darajasi ikkiga teng. x 1 kuchga, y esa 1 kuchga ega, shuning uchun bu muddatning barcha o'zgaruvchilari kuchlarining yig'indisi bo'lgan umumiy daraja 1 + 1 = 2 ga teng. Shuning uchun bu tenglama chiziqli tenglama emas .

• 2x + 3y + 7z + 9c = 20

Bu tenglamada 5 ta had bor, lekin bu barcha atamalarning darajasi 1 ga teng, shuning uchun bu chiziqli tenglama.

Bu erda biz chiziqli tenglama uchun tenglamadagi bir qator o'zgaruvchilarga hech qanday cheklov yo'qligini bilib oldik. Cheklov tenglamadagi atama ega bo'lishi mumkin bo'lgan eng yuqori quvvatga bog'liq.

• \(\mathbf{\frac{2}{x} + y = 10}\)

Bu tenglamada x ning kuchi -1 (x ^-1 ) ga teng, shuning uchun bu tenglama chiziqli tenglama emas .

Ikki o‘zgaruvchili bir vaqtda chiziqli tenglamalarni yechish

Ikki o'zgaruvchidagi ikkita izchil va mustaqil tenglamalar tizimi quyidagicha echiladi:
Yechish:
11x − 7y = 13 …(i)
x − 7y = 3 …(ii)  

Usul:

1. Noma'lumlardan birini yo'q qiling ( y ni yo'q qilaylik) .
2. Boshqa noma'lumni yeching ( bu erda u x ).
3. Ilgari yo'q qilingan noma'lumning qiymatini toping ( y qiymatini toping )

Noma'lumlardan birini yo'q qilish uchun (1-bosqich) quyidagi usullardan foydalanish mumkin:

• O'zgartirish usuli
• Qo'shish yoki ayirish usuli

O'zgartirish usuli:
Yuqoridagi tenglamalarni shu usul yordamida yechamiz.
Uchun (i) 11x - 7y = 13 ni olamiz
−7y = 13 − 11x
\(y = \frac{(13 - 11x)}{-7} \)
Ikkinchi tenglamadagi y ning o'rnini bosuvchi qiymati.
x − 7y = 3
\(x - 7(\frac{13 - 11x}{-7}) = 3 \)
x + 13 − 11x = 3
−10x = 3 − 13
−10x =−10
Shuning uchun x = 1
\(y = \frac{(13 - 11x)}{-7} \) sifatida bu yerda x qiymatini almashtiring va y qiymatini oling.
\(y = \frac{13 - (11 \times 1)}{-7}\)
\(y = \frac{13 - 11}{-7} \\ y = \frac{-2}{7}\)
Demak, x = 1 va y = -2 ∕ 7 kerakli yechimdir.

Yo'q qilish usuli:
Yechish:
2x + 3y = 10
x + y = 6

1. Ikkala tenglamadagi o'zgaruvchining koeffitsientini bir xil qilib (aytaylik, y) ikkala tenglamani songa ko'paytiring.
   (2x + 3y = 10) × 1
   ( x + y = 6 ) × 3
   Endi ikkala tenglamada y koeffitsienti 3 ga teng.
2. Bitta o'zgaruvchidan xalos bo'lish uchun qo'shing yoki ayiring va keyin faqat bitta o'zgaruvchi qolgan tenglamani yeching (x uchun eching)
   2x + 3y = 10
   3x + 3y = 18
   Birinchi tenglamadan ikkinchi tenglamani ayiring.
   +2x + 3y =+10
   +3x + 3y = +18
   - - -
   ------------------
   −x = -8
   Shunday qilib, x = 8
   y = 6 − x ⇒ y = 6 − 8 = −2
   Demak , x = 8, y = -2

Bir vaqtning o'zida tenglamalarni o'z ichiga olgan so'z masalalari:

1-misol : Muayyan ikki xonali sonning raqamlari yig'indisi 13 ga teng va bu raqam birlik raqamidan 7 marta ko'p. Raqamlarni toping.
X birliklar qatorida, y o'nliklar qatorida bo'lsin.
10y + x = raqam = yx
y + x = 13
10y + x = 2 + 7x ⇒ 10y − 6x = 2
2(5y −3x) = 2 ⇒ 5y − 3x = 1 ⇒ \( y = \frac{1 + 3x}{5}\) … almashtirish usuli yordamida
y + x = 13 ⇒ \(\frac{1 + 3x}{5} + x = 13\)
1 + 3x + 5x = 13 × 5
1 + 8x = 65 ⇒ 8x = 64
x = 8, shuning uchun y = 13 − x ⇒ y = 13 − 8 = 5
Raqam 10 × 5 + 8 = 58 (Javob)

2-misol: 3 ta kofe qutisi va 2 choy paketining narxi 15 dollar, bir xil turdagi bir kofe va 4 choy paketining narxi 12 dollar. Har birining narxini toping.
Bitta kofe qolipining narxi $x va bitta choy paketi uchun $y bo'lsin.
3x + 2y = 16
1x + 4y = 12
Yo'q qilish usulidan foydalaning,
12x + 8y = 64
+2x + 8y = 24
- - -
----------------
10x = 40
x = 4, shuning uchun 4 + 4y = 12 ⇒ y = 2
Bitta kofe qolipining narxi 4 dollar, choy paketining narxi 2 dollar.(Javob)