Một phương trình tuyến tính là một phương trình cho một đường thẳng. Ví dụ: 2x + y = 5 là một phương trình tuyến tính
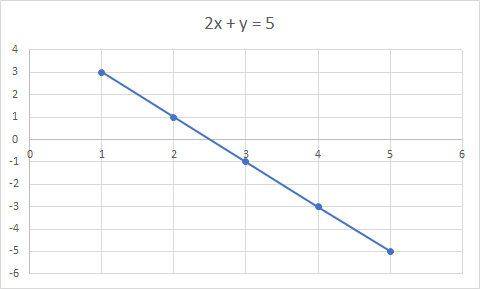
Đồ thị của 2x + y = 5 là một đường thẳng
Chúng ta có thể định nghĩa một phương trình tuyến tính là:
Phương trình tuyến tính là một phương trình bậc 1 và do đó biểu thị một đường thẳng trên đồ thị. Phương trình tuyến tính còn được gọi là phương trình bậc nhất , vì lũy thừa cao nhất của biến trong các phương trình này là 1.
Làm thế nào để chúng ta nói nếu một phương trình là tuyến tính hay không? Hãy hiểu điều này với một vài ví dụ được đưa ra dưới đây.
Thí dụ:
Phương trình nào cũng có bậc. 2x +3y = 5 có ba số hạng. Sức mạnh cao nhất của biến trong một phương trình là 'độ'. Đây là 2x, x có lũy thừa 1 tức là x 1 . Trong 3y, y cũng có lũy thừa 1 tức là y 1 , do đó phương trình này là phương trình tuyến tính
Trong phương trình này, bậc của số hạng 5xy là hai. x có lũy thừa 1, và y có lũy thừa 1 nên tổng bậc, là tổng lũy thừa của tất cả các biến của số hạng đó là 1 + 1 = 2. Do đó, phương trình này không phải là phương trình tuyến tính.
Trong phương trình này có 5 số hạng nhưng bậc của tất cả các số hạng này bằng 1 nên đây là phương trình tuyến tính.
Ở đây chúng ta đã biết rằng đối với Phương trình tuyến tính, không có giới hạn đối với một số biến trong phương trình. Giới hạn nằm ở lũy thừa cao nhất mà một số hạng trong một phương trình có thể có.
Trong phương trình này, lũy thừa của x là -1 (x -1 ), do đó phương trình này không phải là phương trình tuyến tính.
Hệ hai phương trình nhất quán và độc lập hai biến được giải như sau:
Giải quyết:
11x−7y = 13
x−7y = 3
Phương pháp:
Để loại bỏ một trong những phương pháp không xác định (bước 1), có thể sử dụng các phương pháp sau:
Phương pháp thay thế:
Hãy để chúng tôi giải các phương trình trên bằng phương pháp này.
Vì
−7y = 13 − 11x
\(y = \frac{(13 - 11x)}{-7} \)
Giá trị thay thế của y trong phương trình thứ hai.
x−7y = 3
\(x - 7(\frac{13 - 11x}{-7}) = 3 \)
x + 13 − 11x = 3
−10x = 3 − 13
−10x =−10
Do đó, x = 1
dưới dạng \(y = \frac{(13 - 11x)}{-7} \) , thay giá trị của x vào đây và nhận giá trị của y
\(y = \frac{13 - (11 \times 1)}{-7}\)
\(y = \frac{13 - 11}{-7} \\ y = \frac{-2}{7}\)
Do đó, x = 1 và y = −2 ∕ 7 là nghiệm cần thiết.
Phương pháp loại bỏ:
Giải quyết:
2x + 3y = 10
x + y = 6
Ví dụ 1 : Tổng các chữ số của một số có hai chữ số là 13 và chữ số đó gấp 2 lần chữ số hàng đơn vị là 7 lần. Tìm các số.
Gọi x ở hàng đơn vị và y ở hàng chục.
10y + x = số=yx
y + x = 13
10y + x = 2 + 7x ⇒ 10y − 6x = 2
2(5y −3x) = 2 ⇒ 5y − 3x = 1 ⇒ \( y = \frac{1 + 3x}{5}\) … bằng phương pháp thế
y + x = 13 ⇒ \(\frac{1 + 3x}{5} + x = 13\)
1 + 3x + 5x = 13 × 5
1 + 8x = 65 ⇒ 8x = 64
x = 8, do đó y = 13 − x ⇒ y = 13 − 8 = 5
Số đó là 10 × 5 + 8 = 58 (Đáp án)
Ví dụ 2: Giá của 3 hộp cà phê và 2 gói trà là 15 đô la và giá của một hộp cà phê và 4 gói trà cùng loại là 12 đô la. Tìm chi phí của mỗi.
Giả sử giá của một hộp cà phê là x đô la và giá của một gói trà là y đô la.
3x + 2y = 16
1x + 4y = 12
Sử dụng phương pháp loại bỏ,
+2x + 8y = 24
- - -
----------------
10x = 40
x = 4, do đó 4 + 4y = 12 ⇒ y = 2
Giá của một hộp cà phê là 4 đô la và giá của một gói trà là 2 đô la. (Trả lời)