نظرًا لأننا نعرف كيفية قياس الزاوية الحادة للمثلث القائم كنسبة أضلاعه ، فقد حان الوقت لتعلم النسب المثلثية إلى أي زاوية من حيث قياس الراديان ودراستها كوظائف مثلثية.
ضع في اعتبارك دائرة نصف قطرها وحدة ، مركزها عند نقطة أصل محاور الإحداثيات.
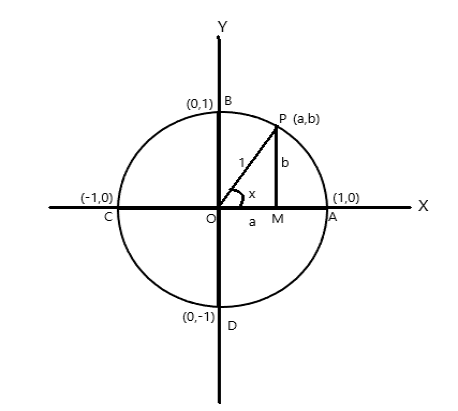
نقاط التنسيق A = (1،0) ، B = (0،1) ، C = (-1،0) و D = (0 ، -1)
لنفترض أن P (a، b) هي أي نقطة على الدائرة مع راديان \(\angle AOP = x \) . لذلك طول القوس \(AP = x \) وحدة.
\(\cos x = a\) ، \(\sin x = b\) . بما أن \(\bigtriangleup POM\) مثلث قائم الزاوية ، \(OP^2 = OM^2 + PM^2\)
لذلك \(1 = a^2 + b^2\)
| \(\mathbf{ \cos^2 x + \sin^2x = 1}\) |
بما أن إحدى الدورات الكاملة تقابل مركز الدائرة زاوية مقدارها \(2\pi\) راديان. من الشكل أعلاه
\(\angle AOB = \pi/2 \)
\(\angle AOC = \pi\)
\(\angle AOD = \frac{3\pi}{2} \)
نحن نعلم \(\cos x = \frac {\textrm {Base}}{\textrm{Hypotenuse}}\) و \(\sin x = \frac {\textrm {Perpendicular}}{\textrm{Hypotenuse}}\)
\(\cos0^\circ = 1\) \(\sin0^\circ = 0\)
\(\cos\frac{\pi}{2} = 0\) \(\sin\frac{\pi}{2} = 1\)
\(\cos\pi = -1\) \(\sin\pi = 0\)
\(\cos2\pi = 1\) \(\sin2\pi = 0\)
عندما نأخذ ثورة كاملة من النقطة P ، نصل مرة أخرى إلى النقطة P. تظل قيمة \(\cos x\) و \(\sin x\) كما هي ، ومن ثم يمكننا أن نقول ذلك
عندما تزيد x أو تنقص بمضاعف متكامل لـ \(2\pi\) ، لا تتغير قيمة دالة الجيب وجيب التمام. هكذا،
\(\sin(n\cdot2\pi + x) = \sin x\)
\(\cos(n\cdot 2\pi + x) = \cos x \)
أين ن عدد صحيح.
سنلاحظ أن \(\sin x = 0\) عندما \(\space x = n\pi\)
و \(\cos x = 0\) عندما \(x = (2n+1)\pi/2\)
اشتقاق الدوال المثلثية الأخرى من حيث دوال الجيب وجيب التمام.
| \(\mathbf{\csc x} = \mathbf{\frac{1}{\sin x}}\) حيث \(x \neq n\pi\) |
| \(\mathbf{\sec x } = \mathbf{\frac{1}{\cos x}}\) حيث |
| \(\mathbf{\tan x } = \mathbf{\frac{\sin x}{\cos x}}\) حيث |
| \(\mathbf{\cot x } = \mathbf{\frac{\cos x}{\sin x}}\) حيث \( x \neq n\pi\) |
| \(\textbf 1 + \mathbf {\tan^2x = \sec^2x}\) |
| \(\textbf 1 + \mathbf {\cot^2x = \csc^2x}\) |
يوضح الجدول أدناه كيف تتغير علامة وقيمة الدوال المثلثية في الأرباع المختلفة.
| الأرباع | أنا | ثانيًا | ثالثا | رابعا |
| sinx | + | + | - | - |
| كوسكس | + | - | - | + |
| تانكس | + | - | + | - |
| cosecx | + | + | - | - |
| secx | + | - | - | + |
| كوتكس | + | - | + | - |
ألق نظرة على الجدول أدناه الذي يوضح قيمة الزوايا المثلثية للدرجات مثل 0 درجة و 30 درجة و 45 درجة و 60 درجة و 90 درجة.
الزوايا (بالدرجات والراديان) | الخطيئة | كوس | تان | سرير نقال | CSC | ثانية |
| 0 درجة | 0 | 1 | 0 | ∞ | ∞ | 1 |
| 30 درجة أو π / 6 راديان | 1/2 | √3 / 2 | 1 / √3 | √3 | 2 | 2 / √3 |
| 45 درجة أو π / 4 راديان | 1/2 | 1/2 | 1 | 1 | √2 | √2 |
| 60 درجة أو π / 3 راديان | √3 / 2 | 1/2 | √3 | 1 / √3 | 2 / √3 | 2 |
| 90 درجة أو π / 2 راديان | 1 | 0 | ∞ | 0 | 1 | ∞ |
| 180 درجة أو π راديان | 0 | -1 | 0 | ∞ | ∞ | -1 |
| 270 درجة أو 3π / 2 راديان | -1 | 0 | ∞ | 0 | -1 | ∞ |
| 360 درجة أو 2 درجة راديان | 0 | 1 | 0 | ∞ | ∞ | 1 |
انظر إلى الجدول أعلاه ، ستلاحظ ما يلي:
\(\mathbf{\sin x = \cos(90^\circ-x)}\) |
| \(\mathbf{\tan x = \cot(90^\circ-x)}\) |
| \(\mathbf{\sec x = \csc(90^\circ-x) }\) |
| \(\mathbf{\csc x = \sec(90^\circ-x)}\) |
| \( \mathbf{ \sin(-x) = -\sin x}\) |
| \( \mathbf{ \cos(-x) = \cos x}\) |
| \(\tan(-x) = -\tan x\) |
تمثيل رسومي لـ \(\sin x\) و \(\cos x\) حيث تتراوح y من -1 إلى +1 عندما تأخذ x قيمًا من \(-3\pi \) إلى \(3\pi \) . تتكرر قيم الجيب وجيب التمام للوظيفة المثلثية بعد فاصل زمني من \(2\pi \) .
يظهر الجيب كخط متصل وجيب التمام كخط منقط.
دعونا نحل بعض الأمثلة بناءً على الدوال المثلثية المذكورة أعلاه:
مثال 1: إذا كان \(\cos x\) = - 4/5 ، x تقع في الربع الثالث ، فأوجد قيم الدوال المثلثية الخمس الأخرى.
الحل: راجع الجداول الواردة أعلاه.
كـ \(\cos x\) = -4/5 ، لذلك \(\sec x\) = -5/4
كـ \(\mathbf{ \cos^2 x + \sin^2x = 1}\) لذا \({16\over25} + \sin^2x = 1 ⇒ \sin^2x = 1-\frac{16}{25} = {9\over25}\)
\(\sin x = \pm3/5\)
نظرًا لأن x تكمن في قيمة الربع الثالث ، فإن \(\sin x\) سيكون سالبًا (راجع جدول الإشارة الرباعي). لذلك \(\sin x\) = -3/5 و \(\csc x \) = -5/3
كـ \(\tan x = \sin x/\cos x\) ، لذلك \(\tan x\) = \(\frac{-4/5}{-3/5}\) = 4/3
مثال 2: أوجد قيمة \(\cos(5\pi/2)\)
حل: \(\cos(5\pi/2) = \cos (2\pi + {1\pi}/_2)\)
نظرًا لتكرار قيمة جيب التمام بعد \(2\pi \) \(\cos(2\pi + {1\pi}/_2) = \cos(\pi/2) = 0\)