Düzbucaqlı üçbucaq üçün iti bucağı onun tərəflərinin nisbəti kimi necə ölçəcəyimizi bildiyimizə görə, radian ölçüsü baxımından istənilən bucağa triqonometrik nisbətləri öyrənmək və onları triqonometrik funksiyalar kimi öyrənmək vaxtıdır.
Mərkəzi koordinat oxlarının başlanğıcında olan vahid radiuslu dairəni nəzərdən keçirək.
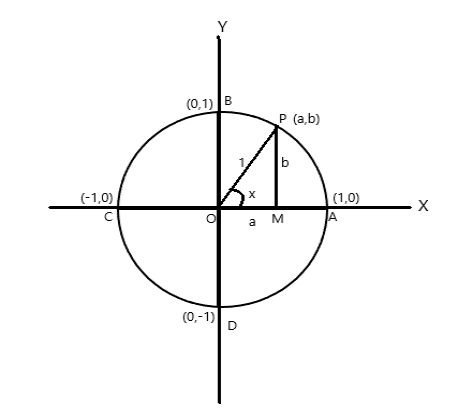
A = (1,0), B = (0,1), C = (-1,0) və D = (0,-1) koordinat nöqtələri
P (a,b) dairənin \(\angle AOP = x \) radian olan istənilən nöqtəsi olsun. Buna görə də qövsün uzunluğu \(AP = x \) vahididir.
\(\cos x = a\) , \(\sin x = b\) . \(\bigtriangleup POM\) düzbucaqlı üçbucaq olduğundan, \(OP^2 = OM^2 + PM^2\)
buna görə \(1 = a^2 + b^2\)
| \(\mathbf{ \cos^2 x + \sin^2x = 1}\) |
Tam bir inqilab dairənin mərkəzində \(2\pi\) radian bucaq altında olduğundan. Yuxarıdakı rəqəmdən
\(\angle AOB = \pi/2 \)
\(\angle AOC = \pi\)
\(\angle AOD = \frac{3\pi}{2} \)
Biz bilirik \(\cos x = \frac {\textrm {Base}}{\textrm{Hypotenuse}}\) və \(\sin x = \frac {\textrm {Perpendicular}}{\textrm{Hypotenuse}}\)
\(\cos0^\circ = 1\) \(\sin0^\circ = 0\)
\(\cos\frac{\pi}{2} = 0\) \(\sin\frac{\pi}{2} = 1\)
\(\cos\pi = -1\) \(\sin\pi = 0\)
\(\cos2\pi = 1\) \(\sin2\pi = 0\)
P nöqtəsindən tam bir inqilab etdikdə yenidən P nöqtəsinə çatırıq \(\cos x\) və \(\sin x\) dəyəri eyni qalır, ona görə də deyə bilərik ki,
x \(2\pi\) inteqral qatı artdıqca və ya azaldıqca sinusun, kosinus funksiyasının qiyməti dəyişmir. Beləliklə,
\(\sin(n\cdot2\pi + x) = \sin x\)
\(\cos(n\cdot 2\pi + x) = \cos x \)
burada n tam ədəddir.
Biz qeyd edəcəyik ki, \(\sin x = 0\) zaman \(\space x = n\pi\)
və \(\cos x = 0\) olduqda \(x = (2n+1)\pi/2\)
Sinus və kosinus funksiyaları baxımından digər triqonometrik funksiyaların çıxarılması.
| \(\mathbf{\csc x} = \mathbf{\frac{1}{\sin x}}\) burada \(x \neq n\pi\) |
| \(\mathbf{\sec x } = \mathbf{\frac{1}{\cos x}}\) burada |
| \(\mathbf{\tan x } = \mathbf{\frac{\sin x}{\cos x}}\) burada |
| \(\mathbf{\cot x } = \mathbf{\frac{\cos x}{\sin x}}\) burada \( x \neq n\pi\) |
| \(\textbf 1 + \mathbf {\tan^2x = \sec^2x}\) |
| \(\textbf 1 + \mathbf {\cot^2x = \csc^2x}\) |
Aşağıdakı cədvəl triqonometrik funksiyaların işarəsi və qiymətinin müxtəlif kvadrantlarda necə dəyişdiyini göstərir.
| Kvadrantlar | I | II | III | IV |
| sinx | + | + | − | − |
| cosx | + | − | − | + |
| tanx | + | − | + | − |
| cosecx | + | + | − | − |
| sekx | + | − | − | + |
| cotx | + | − | + | − |
0°, 30°, 45°, 60° və 90° kimi dərəcələr üçün triqonometrik açıların dəyərini göstərən aşağıdakı cədvələ nəzər salın.
Bucaqlar (dərəcə və radyanla) | sin | cos | tan | cot | csc | san |
| 0° | 0 | 1 | 0 | ∞ | ∞ | 1 |
| 30° və ya π/6 radian | 1/2 | √3/2 | 1/√3 | √3 | 2 | 2/√3 |
| 45 ° və ya π/4 radian | 1/√2 | 1/√2 | 1 | 1 | √2 | √2 |
| 60° və ya π/3 radian | √3/2 | 1/2 | √3 | 1/ √3 | 2/√3 | 2 |
| 90° və ya π/2 radian | 1 | 0 | ∞ | 0 | 1 | ∞ |
| 180° və ya π radian | 0 | -1 | 0 | ∞ | ∞ | -1 |
| 270° və ya 3π/2 | radian | -1 | 0 | ∞0 | - 1 | ∞ |
| 360° və ya 2π radian | 0 | 1 | 0 | ∞ | ∞ | 1 |
Yuxarıdakı cədvələ diqqət yetirin, görəcəksiniz ki:
\mathbf{\tan x = \cot(90^\circ)\(\mathbf{\sin x = \cos(90^\circ-x)}\) |
| \(\mathbf{\tan x = \cot(90^\circ-x)}\) |
| \(\mathbf{\tan x = \cot(90^\circ-x)}\) |
| \(\mathbf{\sec x = \csc(90^\circ-x) }\) |
| \(\mathbf{\csc x = \sec(90^\circ-x)}\) |
| \( \mathbf{ \sin(-x) = -\sin x}\) |
| \( \mathbf{ \cos(-x) = \cos x}\) |
| \(\tan(-x) = -\tan x\) |
\(\sin x\) və \(\cos x\) qrafik təsviri, burada x \(-3\pi \) ilə \(3\pi \) arasında dəyərlər qəbul edərkən y -1 ilə +1 arasında dəyişir. . Həm triqonometrik funksiyanın sinus, həm də kosinus dəyərləri \(2\pi \) intervaldan sonra təkrarlanır.
Sinus düz xətt, kosinus isə nöqtəli xətt kimi göstərilir.
Yuxarıdakı triqonometrik funksiyalara əsaslanaraq bir neçə nümunə həll edək:
Misal 1: Əgər \(\cos x\) = − 4/5, x üçüncü kvadrantda yerləşirsə, digər beş triqonometrik funksiyanın qiymətlərini tapın.
Həlli: Yuxarıda verilmiş cədvəllərə baxın.
\(\cos x\) = -4/5, buna görə \(\sec x\) = -5/4
\(\mathbf{ \cos^2 x + \sin^2x = 1}\) olduğu kimi \({16\over25} + \sin^2x = 1 ⇒ \sin^2x = 1-\frac{16}{25} = {9\over25}\)
\(\sin x = \pm3/5\)
X üçüncü kvadrant dəyərində olduğu üçün \(\sin x\) mənfi olacaq (kvadrant işarəsi cədvəlinə baxın). Buna görə \(\sin x\) = -3/5 və \(\csc x \) = -5/3
\(\tan x = \sin x/\cos x\) kimi, buna görə də \(\tan x\) = \(\frac{-4/5}{-3/5}\) = 4/3 Nümunə
2 : \(\cos(5\pi/2)\) dəyərini tapın
Həll: \(\cos(5\pi/2) = \cos (2\pi + {1\pi}/_2)\)
Kosinusun dəyəri \(2\pi \) sonra təkrarlandığı üçün, \(\cos(2\pi + {1\pi}/_2) = \cos(\pi/2) = 0\)