যেহেতু আমরা জানি কিভাবে সমকোণ ত্রিভুজের বাহুর অনুপাত হিসাবে একটি তীব্র কোণ পরিমাপ করা যায়, রেডিয়ান পরিমাপের পরিপ্রেক্ষিতে যেকোন কোণের ত্রিকোণমিতিক অনুপাত শেখার এবং ত্রিকোণমিতিক ফাংশন হিসাবে অধ্যয়ন করার সময় এসেছে।
একক ব্যাসার্ধের একটি বৃত্ত বিবেচনা করুন, যার কেন্দ্র স্থানাঙ্ক অক্ষের উৎপত্তিস্থলে অবস্থিত।
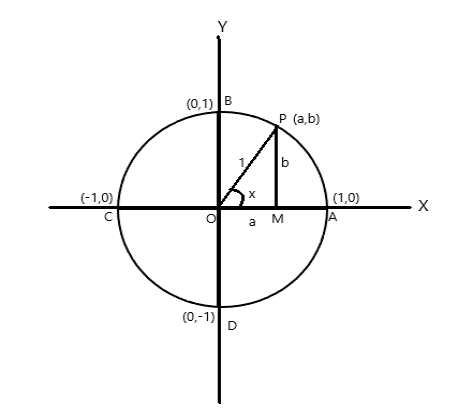
A = (1,0), B = (0,1), C = (-1,0) এবং D = (0,-1) এর স্থানাঙ্ক বিন্দু।
P (a,b) কে \(\angle AOP = x \) রেডিয়ান সহ বৃত্তের যেকোনো বিন্দু হতে দিন। তাই চাপের দৈর্ঘ্য \(AP = x \) একক।
\(\cos x = a\) , \(\sin x = b\) । যেহেতু \(\bigtriangleup POM\) একটি সমকোণ ত্রিভুজ, \(OP^2 = OM^2 + PM^2\)
অতএব \(1 = a^2 + b^2\)
| \(\mathbf{ \cos^2 x + \sin^2x = 1}\) |
যেহেতু একটি সম্পূর্ণ বিপ্লব বৃত্তের কেন্দ্রে \(2\pi\) রেডিয়ানের একটি কোণ করে। উপরের চিত্র থেকে
\(\angle AOB = \pi/2 \)
\(\angle AOC = \pi\)
\(\angle AOD = \frac{3\pi}{2} \)
আমরা জানি \(\cos x = \frac {\textrm {Base}}{\textrm{Hypotenuse}}\) এবং \(\sin x = \frac {\textrm {Perpendicular}}{\textrm{Hypotenuse}}\)
\(\cos0^\circ = 1\) \(\sin0^\circ = 0\)
\(\cos\frac{\pi}{2} = 0\) \(\sin\frac{\pi}{2} = 1\)
\(\cos\pi = -1\) \(\sin\pi = 0\)
\(\cos2\pi = 1\) \(\sin2\pi = 0\)
যখন আমরা P বিন্দু থেকে একটি সম্পূর্ণ ক্রান্তি নিই তখন আমরা আবার P বিন্দুতে পৌঁছাই \(\cos x\) এবং \(\sin x\) এর মান একই থাকে, তাই আমরা বলতে পারি যে
x যেহেতু \(2\pi\) এর একটি অবিচ্ছেদ্য গুণিতক দ্বারা বৃদ্ধি বা হ্রাস পায়, সাইন, কোসাইন ফাংশনের মান পরিবর্তন হয় না। এইভাবে,
\(\sin(n\cdot2\pi + x) = \sin x\)
\(\cos(n\cdot 2\pi + x) = \cos x \)
যেখানে n একটি পূর্ণসংখ্যা।
আমরা লক্ষ্য করব যে \(\sin x = 0\) যখন \(\space x = n\pi\)
এবং \(\cos x = 0\) যখন \(x = (2n+1)\pi/2\)
সাইন এবং কোসাইন ফাংশনের পরিপ্রেক্ষিতে অন্যান্য ত্রিকোণমিতিক ফাংশন প্রাপ্ত করা।
| \(\mathbf{\csc x} = \mathbf{\frac{1}{\sin x}}\) যেখানে \(x \neq n\pi\) |
| \(\mathbf{\sec x } = \mathbf{\frac{1}{\cos x}}\) যেখানে |
| \(\mathbf{\tan x } = \mathbf{\frac{\sin x}{\cos x}}\) যেখানে |
| \(\mathbf{\cot x } = \mathbf{\frac{\cos x}{\sin x}}\) যেখানে \( x \neq n\pi\) |
| \(\textbf 1 + \mathbf {\tan^2x = \sec^2x}\) |
| \(\textbf 1 + \mathbf {\cot^2x = \csc^2x}\) |
নীচের সারণী দেখায় কিভাবে ত্রিকোণমিতিক ফাংশনের চিহ্ন এবং মান বিভিন্ন চতুর্ভুজে পরিবর্তিত হয়।
| চতুর্ভুজ | আমি | ২ | III | IV |
| sinx | + | + | - | - |
| cosx | + | - | - | + |
| ট্যানক্স | + | - | + | - |
| cosecx | + | + | - | - |
| সেক্স | + | - | - | + |
| cotx | + | - | + | - |
নীচের সারণীটি দেখুন যা 0°, 30°, 45°, 60° এবং 90° এর মতো ডিগ্রীর জন্য ত্রিকোণমিতিক কোণের মান দেখায়।
কোণ (ডিগ্রী এবং রেডিয়ানে) | পাপ | কারণ | ট্যান | খাট | csc | সেকেন্ড |
| 0° | 0 | 1 | 0 | ∞ | ∞ | 1 |
| 30° বা π/6 রেডিয়ান | 1/2 | √3/2 | 1/√3 | √3 | 2 | 2/√3 |
| 45° বা π/4 রেডিয়ান | 1/√2 | 1/√2 | 1 | 1 | √2 | √2 |
| 60° বা π/3 রেডিয়ান | √3/2 | 1/2 | √3 | 1/√3 | 2/√3 | 2 |
| 90° বা π/2 রেডিয়ান | 1 | 0 | ∞ | 0 | 1 | ∞ |
| 180° বা π রেডিয়ান | 0 | -1 | 0 | ∞ | ∞ | -1 |
| 270° বা 3π/2 রেডিয়ান | -1 | 0 | ∞ | 0 | -1 | ∞ |
| 360° বা 2π রেডিয়ান | 0 | 1 | 0 | ∞ | ∞ | 1 |
উপরের টেবিলটি পর্যবেক্ষণ করুন, আপনি লক্ষ্য করবেন যে:
\(\mathbf{\sin x = \cos(90^\circ-x)}\) |
| \(\mathbf{\tan x = \cot(90^\circ-x)}\) |
| \(\mathbf{\sec x = \csc(90^\circ-x) }\) |
| \(\mathbf{\csc x = \sec(90^\circ-x)}\) |
| \( \mathbf{ \sin(-x) = -\sin x}\) |
| \( \mathbf{ \cos(-x) = \cos x}\) |
| \(\tan(-x) = -\tan x\) |
\(\sin x\) এবং \(\cos x\) এর গ্রাফিকাল উপস্থাপনা যেখানে y রেঞ্জ -1 থেকে +1 পর্যন্ত যখন x \(-3\pi \) থেকে \(3\pi \) পর্যন্ত মান নেয়। ত্রিকোণমিতিক ফাংশন সাইন এবং কোসাইন মান উভয়ই \(2\pi \) এর ব্যবধানের পরে পুনরাবৃত্তি করে।
সাইন একটি কঠিন রেখা হিসাবে এবং কোসাইন একটি বিন্দুযুক্ত রেখা হিসাবে দেখানো হয়েছে।
আসুন উপরের ত্রিকোণমিতিক ফাংশনের উপর ভিত্তি করে কয়েকটি উদাহরণ সমাধান করি:
উদাহরণ 1: যদি \(\cos x\) = − 4/5, x তৃতীয় চতুর্ভুজে থাকে, অন্য পাঁচটি ত্রিকোণমিতিক ফাংশনের মান খুঁজুন।
সমাধান: উপরে দেওয়া সারণীগুলি পড়ুন।
যেমন \(\cos x\) = -4/5, অতএব \(\sec x\) = -5/4
যেমন \(\mathbf{ \cos^2 x + \sin^2x = 1}\) তাই \({16\over25} + \sin^2x = 1 ⇒ \sin^2x = 1-\frac{16}{25} = {9\over25}\)
\(\sin x = \pm3/5\)
যেহেতু x তৃতীয় চতুর্ভুজ মানের মধ্যে রয়েছে, তাই \(\sin x\) ঋণাত্মক হবে (চতুর্ভুজ চিহ্নের টেবিলটি পড়ুন)। অতএব \(\sin x\) = -3/5 এবং \(\csc x \) = -5/3
যেমন \(\tan x = \sin x/\cos x\) , অতএব \(\tan x\) = \(\frac{-4/5}{-3/5}\) = 4/3
উদাহরণ 2: \(\cos(5\pi/2)\) এর মান খুঁজুন
সমাধান: \(\cos(5\pi/2) = \cos (2\pi + {1\pi}/_2)\)
যেহেতু কোসাইনের মান \(2\pi \) এর পরে পুনরাবৃত্তি \(\cos(2\pi + {1\pi}/_2) = \cos(\pi/2) = 0\)