Da wir wissen, wie man einen spitzen Winkel für das rechtwinklige Dreieck als Verhältnis seiner Seiten misst, ist es an der Zeit, trigonometrische Verhältnisse zu jedem Winkel im Bogenmaß zu lernen und sie als trigonometrische Funktionen zu studieren.
Betrachten Sie einen Kreis mit einem Einheitsradius, dessen Mittelpunkt im Ursprung der Koordinatenachsen liegt.
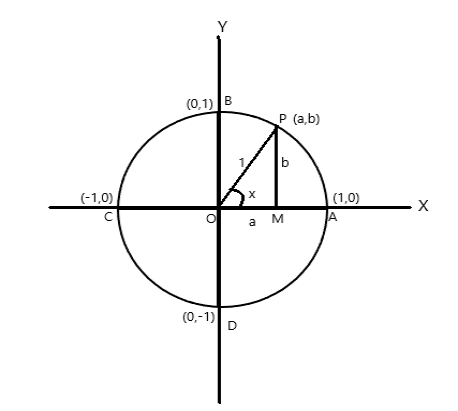
Koordinatenpunkte von A = (1,0), B = (0,1), C = (-1,0) und D = (0,-1)
Sei P (a,b) ein beliebiger Punkt auf dem Kreis mit \(\angle AOP = x \) im Bogenmaß. Daher ist die Bogenlänge \(AP = x \) Einheit.
\(\cos x = a\) , \(\sin x = b\) . Da \(\bigtriangleup POM\) ein rechtwinkliges Dreieck ist, \(OP^2 = OM^2 + PM^2\)
also \(1 = a^2 + b^2\)
| \(\mathbf{ \cos^2 x + \sin^2x = 1}\) |
Da eine vollständige Umdrehung im Mittelpunkt des Kreises einen Winkel von \(2\pi\) Bogenmaß einschließt. Aus der obigen Abbildung
\(\angle AOB = \pi/2 \)
\(\angle AOC = \pi\)
\(\angle AOD = \frac{3\pi}{2} \)
Wir wissen \(\cos x = \frac {\textrm {Base}}{\textrm{Hypotenuse}}\) und \(\sin x = \frac {\textrm {Perpendicular}}{\textrm{Hypotenuse}}\)
\(\cos0^\circ = 1\) \(\sin0^\circ = 0\)
\(\cos\frac{\pi}{2} = 0\) \(\sin\frac{\pi}{2} = 1\)
\(\cos\pi = -1\) \(\sin\pi = 0\)
\(\cos2\pi = 1\) \(\sin2\pi = 0\)
Wenn wir von Punkt P aus eine vollständige Umdrehung machen, erreichen wir wieder Punkt P. Der Wert von \(\cos x\) und \(\sin x\) bleibt derselbe, daher können wir das sagen
Wenn x um ein ganzzahliges Vielfaches von \(2\pi\) zunimmt oder abnimmt, ändert sich der Wert der Sinus- und Cosinusfunktion nicht. Daher,
\(\sin(n\cdot2\pi + x) = \sin x\)
\(\cos(n\cdot 2\pi + x) = \cos x \)
wobei n eine ganze Zahl ist.
Wir werden feststellen, dass \(\sin x = 0\) wenn \(\space x = n\pi\)
und \(\cos x = 0\) , wenn \(x = (2n+1)\pi/2\)
Ableitung anderer trigonometrischer Funktionen in Form von Sinus- und Cosinusfunktionen.
| \(\mathbf{\csc x} = \mathbf{\frac{1}{\sin x}}\) wobei \(x \neq n\pi\) |
| \(\mathbf{\sec x } = \mathbf{\frac{1}{\cos x}}\) wobei |
| \(\mathbf{\tan x } = \mathbf{\frac{\sin x}{\cos x}}\) wobei |
| \(\mathbf{\cot x } = \mathbf{\frac{\cos x}{\sin x}}\) wobei \( x \neq n\pi\) |
| \(\textbf 1 + \mathbf {\tan^2x = \sec^2x}\) |
| \(\textbf 1 + \mathbf {\cot^2x = \csc^2x}\) |
Die folgende Tabelle zeigt, wie sich Vorzeichen und Wert trigonometrischer Funktionen in verschiedenen Quadranten ändern.
| Quadranten | ICH | II | III | IV |
| sinx | + | + | − | − |
| cosx | + | − | − | + |
| tanx | + | − | + | − |
| cosecx | + | + | − | − |
| secx | + | − | − | + |
| cotx | + | − | + | − |
Schauen Sie sich die folgende Tabelle an, die den Wert der trigonometrischen Winkel für Grad wie 0°, 30°, 45°, 60° und 90° zeigt.
Winkel (in Grad und Bogenmaß) | Sünde | cos | bräunen | Kinderbett | csc | Sek |
| 0° | 0 | 1 | 0 | ∞ | ∞ | 1 |
| 30° oder π/6 Bogenmaß | 1/2 | √3/2 | 1/√3 | √3 | 2 | 2/√3 |
| 45° oder π/4 Bogenmaß | 1/√2 | 1/√2 | 1 | 1 | √2 | √2 |
| 60° oder π/3 Bogenmaß | √3/2 | 1/2 | √3 | 1/√3 | 2/√3 | 2 |
| 90° oder π/2 Bogenmaß | 1 | 0 | ∞ | 0 | 1 | ∞ |
| 180° oder π Bogenmaß | 0 | -1 | 0 | ∞ | ∞ | -1 |
| 270° oder 3π/2 Bogenmaß | -1 | 0 | ∞ | 0 | -1 | ∞ |
| 360° oder 2π Bogenmaß | 0 | 1 | 0 | ∞ | ∞ | 1 |
Beachten Sie die obige Tabelle. Sie werden Folgendes feststellen:
\(\mathbf{\sin x = \cos(90^\circ-x)}\) |
| \(\mathbf{\tan x = \cot(90^\circ-x)}\) |
| \(\mathbf{\sec x = \csc(90^\circ-x) }\) |
| \(\mathbf{\csc x = \sec(90^\circ-x)}\) |
| \( \mathbf{ \sin(-x) = -\sin x}\) |
| \( \mathbf{ \cos(-x) = \cos x}\) |
| \(\tan(-x) = -\tan x\) |
Grafische Darstellung von \(\sin x\) und \(\cos x\) wobei y von -1 bis +1 reicht, wenn x Werte von \(-3\pi \) bis \(3\pi \) annimmt. Sowohl der Sinus- als auch der Kosinuswert der trigonometrischen Funktion wiederholen sich nach einem Intervall von \(2\pi \) .
Sinus wird als durchgezogene Linie und Cosinus als gepunktete Linie dargestellt.
Lassen Sie uns einige Beispiele basierend auf den oben genannten trigonometrischen Funktionen lösen:
Beispiel 1: Wenn \(\cos x\) = − 4/5, x im dritten Quadranten liegt, ermitteln Sie die Werte der anderen fünf trigonometrischen Funktionen.
Lösung: Sehen Sie sich die oben aufgeführten Tabellen an.
Da \(\cos x\) = -4/5, also \(\sec x\) = -5/4
Da \(\mathbf{ \cos^2 x + \sin^2x = 1}\) also \({16\over25} + \sin^2x = 1 ⇒ \sin^2x = 1-\frac{16}{25} = {9\over25}\)
\(\sin x = \pm3/5\)
Da x im dritten Quadrantenwert liegt, ist \(\sin x\) negativ (siehe Quadrantenvorzeichentabelle). Daher \(\sin x\) = -3/5 und \(\csc x \) = -5/3
Da \(\tan x = \sin x/\cos x\) , also \(\tan x\) = \(\frac{-4/5}{-3/5}\) = 4/3
Beispiel 2: Ermitteln Sie den Wert von \(\cos(5\pi/2)\)
Lösung: \(\cos(5\pi/2) = \cos (2\pi + {1\pi}/_2)\)
Da sich der Wert des Kosinus nach \(2\pi \) wiederholt, gilt daher \(\cos(2\pi + {1\pi}/_2) = \cos(\pi/2) = 0\)