As we know how to measure an acute angle for the right triangle as the ratio of its sides, it is time to learn trigonometric ratios to any angle in terms of radian measure and study them as trigonometric functions.
Consider a circle of unit radius, whose center is at the coordinate axes origin.
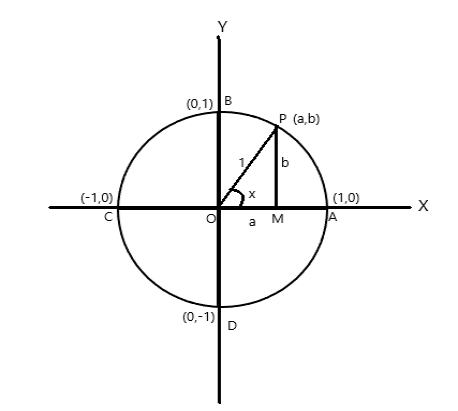
Coordinate points of A = (1,0), B = (0,1), C = (-1,0) and D = (0,-1)
Let P (a,b) be any point on the circle with \(\angle AOP = x \) radian. Therefore the length of arc \(AP = x \) unit.
\(\cos x = a\) , \(\sin x = b\). As \(\bigtriangleup POM\) is a right-angle triangle, \(OP^2 = OM^2 + PM^2\)
therefore \(1 = a^2 + b^2\)
| \(\mathbf{ \cos^2 x + \sin^2x = 1}\) |
Since one complete revolution subtends at the center of the circle an angle of \(2\pi\) radian. From the above figure
\(\angle AOB = \pi/2 \)
\(\angle AOC = \pi\)
\(\angle AOD = \frac{3\pi}{2} \)
We know \(\cos x = \frac {\textrm {Base}}{\textrm{Hypotenuse}}\) and \(\sin x = \frac {\textrm {Perpendicular}}{\textrm{Hypotenuse}}\)
\(\cos0^\circ = 1\) \(\sin0^\circ = 0\)
\(\cos\frac{\pi}{2} = 0\) \(\sin\frac{\pi}{2} = 1\)
\(\cos\pi = -1\) \(\sin\pi = 0\)
\(\cos2\pi = 1\) \(\sin2\pi = 0\)
As we take one complete revolution from point P we again reach point P. The value of \(\cos x\) and \(\sin x\) remains the same, hence we can say that
as x increases or decreases by an integral multiple of \(2\pi\), the value of sine, cosine function does not change. Thus,
\(\sin(n\cdot2\pi + x) = \sin x\)
\(\cos(n\cdot 2\pi + x) = \cos x \)
where n is an integer.
We will notice that \(\sin x = 0\) when \(\space x = n\pi\)
and \(\cos x = 0\) when \(x = (2n+1)\pi/2\)
Deriving other trigonometric functions in terms of sine and cosine functions.
| \(\mathbf{\csc x} = \mathbf{\frac{1}{\sin x}}\) where \(x \neq n\pi\) |
| \(\mathbf{\sec x } = \mathbf{\frac{1}{\cos x}}\) where |
| \(\mathbf{\tan x } = \mathbf{\frac{\sin x}{\cos x}}\) where |
| \(\mathbf{\cot x } = \mathbf{\frac{\cos x}{\sin x}}\) where \( x \neq n\pi\) |
| \(\textbf 1 + \mathbf {\tan^2x = \sec^2x}\) |
| \(\textbf 1 + \mathbf {\cot^2x = \csc^2x}\) |
Below table shows how the sign and value of trigonometric functions change in different quadrants.
| Quadrants | I | II | III | IV |
| sinx | + | + | − | − |
| cosx | + | − | − | + |
| tanx | + | − | + | − |
| cosecx | + | + | − | − |
| secx | + | − | − | + |
| cotx | + | − | + | − |
Take a look at the below table which shows the value of trigonometric angles for degrees such as 0°, 30°, 45°, 60°, and 90°.
|
Angles(in degrees & radian) |
sin | cos | tan | cot | csc | sec |
| 0° | 0 | 1 | 0 | ∞ | ∞ | 1 |
| 30° or π/6 radian | 1/2 | √3/2 | 1/√3 | √3 | 2 | 2/√3 |
| 45° or π/4 radian | 1/√2 | 1/√2 | 1 | 1 | √2 | √2 |
| 60° or π/3 radian | √3/2 | 1/2 | √3 | 1/√3 | 2/√3 | 2 |
| 90° or π/2 radian | 1 | 0 | ∞ | 0 | 1 | ∞ |
| 180° or π radian | 0 | -1 | 0 | ∞ | ∞ | -1 |
| 270° or 3π/2 radian | -1 | 0 | ∞ | 0 | -1 | ∞ |
| 360° or 2π radian | 0 | 1 | 0 | ∞ | ∞ | 1 |
Observe the above table, you will notice that:
|
\(\mathbf{\sin x = \cos(90^\circ-x)}\) |
| \(\mathbf{\tan x = \cot(90^\circ-x)}\) |
| \(\mathbf{\sec x = \csc(90^\circ-x) }\) |
| \(\mathbf{\csc x = \sec(90^\circ-x)}\) |
| \( \mathbf{ \sin(-x) = -\sin x}\) |
| \( \mathbf{ \cos(-x) = \cos x}\) |
| \(\tan(-x) = -\tan x\) |
Graphical representation of \(\sin x\) and \(\cos x\) where y ranges from -1 to +1 when x takes values from \(-3\pi \) to \(3\pi \). Both trigonometric function sine and cosine values repeat after an interval of \(2\pi \).
Sine is shown as a solid line and Cosine as a dotted line.
Let us solve a few examples based on the above trigonometric functions:
Example 1: If \(\cos x\) = − 4/5, x lies in the third quadrant, find the values of the other five trigonometric functions.
Solution: Refer to the tables given above.
As \(\cos x\) = -4/5, therefore \(\sec x\) = -5/4
As \(\mathbf{ \cos^2 x + \sin^2x = 1}\) so \({16\over25} + \sin^2x = 1 ⇒ \sin^2x = 1-\frac{16}{25} = {9\over25}\)
\(\sin x = \pm3/5\)
As x lies in third quadrant value, so \(\sin x\) will be negative(refer to the quadrant sign table). Therefore \(\sin x\) = -3/5 and \(\csc x \)= -5/3
As \(\tan x = \sin x/\cos x\) , therefore \(\tan x\)= \(\frac{-4/5}{-3/5}\)= 4/3
Example 2: Find the value of \(\cos(5\pi/2)\)
Solution: \(\cos(5\pi/2) = \cos (2\pi + {1\pi}/_2)\)
As the value of cosine repeats after \(2\pi \) therefore, \(\cos(2\pi + {1\pi}/_2) = \cos(\pi/2) = 0\)