Como sabemos cómo medir un ángulo agudo para el triángulo rectángulo como la razón de sus lados, es hora de aprender las razones trigonométricas de cualquier ángulo en términos de medida en radianes y estudiarlas como funciones trigonométricas.
Considere un círculo de radio unidad, cuyo centro está en el origen de los ejes de coordenadas.
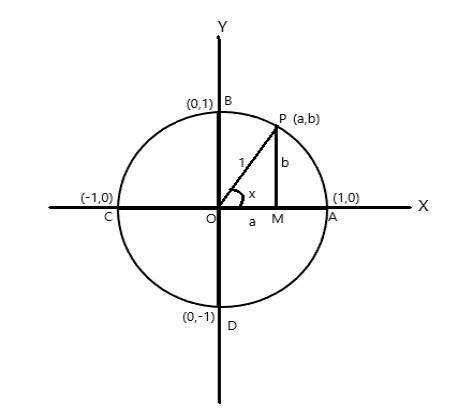
Puntos de coordenadas de A = (1,0), B = (0,1), C = (-1,0) y D = (0,-1)
Sea P (a,b) cualquier punto del círculo con \(\angle AOP = x \) radianes. Por lo tanto la longitud del arco \(AP = x \) unidad.
\(\cos x = a\) , \(\sin x = b\) . Como \(\bigtriangleup POM\) es un triángulo rectángulo, \(OP^2 = OM^2 + PM^2\)
por lo tanto \(1 = a^2 + b^2\)
| \(\mathbf{ \cos^2 x + \sin^2x = 1}\) |
Dado que una revolución completa subtiende en el centro del círculo un ángulo de \(2\pi\) radianes. De la figura anterior
\(\angle AOB = \pi/2 \)
\(\angle AOC = \pi\)
\(\angle AOD = \frac{3\pi}{2} \)
Sabemos \(\cos x = \frac {\textrm {Base}}{\textrm{Hypotenuse}}\) y \(\sin x = \frac {\textrm {Perpendicular}}{\textrm{Hypotenuse}}\)
\(\cos0^\circ = 1\) \(\sin0^\circ = 0\)
\(\cos\frac{\pi}{2} = 0\) \(\sin\frac{\pi}{2} = 1\)
\(\cos\pi = -1\) \(\sin\pi = 0\)
\(\cos2\pi = 1\) \(\sin2\pi = 0\)
Cuando tomamos una revolución completa desde el punto P, nuevamente llegamos al punto P. El valor de \(\cos x\) y \(\sin x\) sigue siendo el mismo, por lo que podemos decir que
a medida que x aumenta o disminuye en un múltiplo entero de \(2\pi\) , el valor de la función seno, coseno no cambia. De este modo,
\(\sin(n\cdot2\pi + x) = \sin x\)
\(\cos(n\cdot 2\pi + x) = \cos x \)
donde n es un número entero.
Notaremos que \(\sin x = 0\) cuando \(\space x = n\pi\)
y \(\cos x = 0\) cuando \(x = (2n+1)\pi/2\)
Derivación de otras funciones trigonométricas en términos de funciones seno y coseno.
| \(\mathbf{\csc x} = \mathbf{\frac{1}{\sin x}}\) donde \(x \neq n\pi\) |
| \(\mathbf{\sec x } = \mathbf{\frac{1}{\cos x}}\) donde |
| \(\mathbf{\tan x } = \mathbf{\frac{\sin x}{\cos x}}\) donde |
| \(\mathbf{\cot x } = \mathbf{\frac{\cos x}{\sin x}}\) donde \( x \neq n\pi\) |
| \(\textbf 1 + \mathbf {\tan^2x = \sec^2x}\) |
| \(\textbf 1 + \mathbf {\cot^2x = \csc^2x}\) |
La siguiente tabla muestra cómo cambian el signo y el valor de las funciones trigonométricas en diferentes cuadrantes.
| cuadrantes | I | Yo | tercero | IV |
| senx | + | + | − | − |
| cosx | + | − | − | + |
| tango | + | − | + | − |
| cosecx | + | + | − | − |
| secx | + | − | − | + |
| cotx | + | − | + | − |
Eche un vistazo a la siguiente tabla que muestra el valor de los ángulos trigonométricos para grados como 0°, 30°, 45°, 60° y 90°.
Ángulos (en grados y radianes) | pecado | porque | broncearse | cuna | csc | segundo |
| 0° | 0 | 1 | 0 | ∞ | ∞ | 1 |
| 30° o π/6 radianes | 1/2 | √3/2 | 1/√3 | √3 | 2 | 2/√3 |
| 45° o π/4 radianes | 1/√2 | 1/√2 | 1 | 1 | √2 | √2 |
| 60° o π/3 radianes | √3/2 | 1/2 | √3 | 1/√3 | 2/√3 | 2 |
| 90° o π/2 radianes | 1 | 0 | ∞ | 0 | 1 | ∞ |
| 180° o π radianes | 0 | -1 | 0 | ∞ | ∞ | -1 |
| 270° o 3π/2 radianes | -1 | 0 | ∞ | 0 | -1 | ∞ |
| 360° o 2π radianes | 0 | 1 | 0 | ∞ | ∞ | 1 |
Observa la tabla anterior, notarás que:
\(\mathbf{\sin x = \cos(90^\circ-x)}\) |
| \(\mathbf{\tan x = \cot(90^\circ-x)}\) |
| \(\mathbf{\sec x = \csc(90^\circ-x) }\) |
| \(\mathbf{\csc x = \sec(90^\circ-x)}\) |
| \( \mathbf{ \sin(-x) = -\sin x}\) |
| \( \mathbf{ \cos(-x) = \cos x}\) |
| \(\tan(-x) = -\tan x\) |
Representación gráfica de \(\sin x\) y \(\cos x\) donde y varía de -1 a +1 cuando x toma valores de \(-3\pi \) a \(3\pi \) . Los valores de seno y coseno de la función trigonométrica se repiten después de un intervalo de \(2\pi \) .
El seno se muestra como una línea continua y el coseno como una línea de puntos.
Resolvamos algunos ejemplos basados en las funciones trigonométricas anteriores:
Ejemplo 1: Si \(\cos x\) = − 4/5, x se encuentra en el tercer cuadrante, encuentra los valores de las otras cinco funciones trigonométricas.
Solución: Consulte las tablas anteriores.
Como \(\cos x\) = -4/5, entonces \(\sec x\) = -5/4
Como \(\mathbf{ \cos^2 x + \sin^2x = 1}\) entonces \({16\over25} + \sin^2x = 1 ⇒ \sin^2x = 1-\frac{16}{25} = {9\over25}\)
\(\sin x = \pm3/5\)
Como x se encuentra en el valor del tercer cuadrante, \(\sin x\) será negativo (consulte la tabla de signos del cuadrante). Por lo tanto \(\sin x\) = -3/5 y \(\csc x \) = -5/3
Como \(\tan x = \sin x/\cos x\) , entonces \(\tan x\) = \(\frac{-4/5}{-3/5}\) = 4/3
Ejemplo 2: Encuentra el valor de \(\cos(5\pi/2)\)
Solución: \(\cos(5\pi/2) = \cos (2\pi + {1\pi}/_2)\)
Como el valor del coseno se repite después de \(2\pi \) , por lo tanto \(\cos(2\pi + {1\pi}/_2) = \cos(\pi/2) = 0\)