همانطور که می دانیم چگونه یک زاویه تند را برای مثلث قائم الزاویه به عنوان نسبت اضلاع آن اندازه گیری کنیم، زمان آن فرا رسیده است که نسبت های مثلثاتی به هر زاویه را از نظر اندازه گیری رادیان یاد بگیریم و آنها را به عنوان توابع مثلثاتی مطالعه کنیم.
دایره ای با شعاع واحد را در نظر بگیرید که مرکز آن در مبدا محورهای مختصات است.
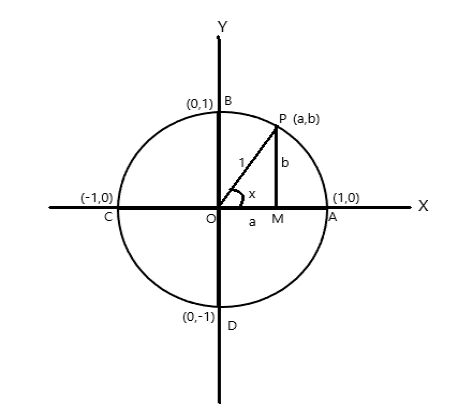
نقاط مختصات A = (1,0)، B = (0,1)، C = (-1,0) و D = (0,-1)
فرض کنید P (a,b) هر نقطه روی دایره با رادیان \(\angle AOP = x \) باشد. بنابراین طول قوس \(AP = x \) واحد است.
\(\cos x = a\) ، \(\sin x = b\) . از آنجایی که \(\bigtriangleup POM\) یک مثلث قائم الزاویه است، \(OP^2 = OM^2 + PM^2\)
بنابراین \(1 = a^2 + b^2\)
| \(\mathbf{ \cos^2 x + \sin^2x = 1}\) |
از آنجایی که یک دور کامل در مرکز دایره زاویه ای برابر با \(2\pi\) رادیان قرار می گیرد. از شکل بالا
\(\angle AOB = \pi/2 \)
\(\angle AOC = \pi\)
\(\angle AOD = \frac{3\pi}{2} \)
ما می دانیم \(\cos x = \frac {\textrm {Base}}{\textrm{Hypotenuse}}\) و \(\sin x = \frac {\textrm {Perpendicular}}{\textrm{Hypotenuse}}\)
\(\cos0^\circ = 1\) \(\sin0^\circ = 0\)
\(\cos\frac{\pi}{2} = 0\) \(\sin\frac{\pi}{2} = 1\)
\(\cos\pi = -1\) \(\sin\pi = 0\)
\(\cos2\pi = 1\) \(\sin2\pi = 0\)
وقتی یک دور کامل از نقطه P می گیریم، دوباره به نقطه P می رسیم. مقدار \(\cos x\) و \(\sin x\) ثابت می ماند، بنابراین می توان گفت که
با افزایش یا کاهش x توسط مضرب انتگرالی \(2\pi\) مقدار سینوس، تابع کسینوس تغییر نمی کند. بدین ترتیب،
\(\sin(n\cdot2\pi + x) = \sin x\)
\(\cos(n\cdot 2\pi + x) = \cos x \)
که در آن n یک عدد صحیح است.
متوجه خواهیم شد که \(\sin x = 0\) وقتی \(\space x = n\pi\)
و \(\cos x = 0\) وقتی \(x = (2n+1)\pi/2\)
استخراج سایر توابع مثلثاتی بر حسب توابع سینوس و کسینوس.
| \(\mathbf{\csc x} = \mathbf{\frac{1}{\sin x}}\) جایی که \(x \neq n\pi\) |
| \(\mathbf{\sec x } = \mathbf{\frac{1}{\cos x}}\) که در آن |
| \(\mathbf{\tan x } = \mathbf{\frac{\sin x}{\cos x}}\) جایی که |
| \(\mathbf{\cot x } = \mathbf{\frac{\cos x}{\sin x}}\) جایی که \( x \neq n\pi\) |
| \(\textbf 1 + \mathbf {\tan^2x = \sec^2x}\) |
| \(\textbf 1 + \mathbf {\cot^2x = \csc^2x}\) |
جدول زیر نشان می دهد که چگونه علامت و مقدار توابع مثلثاتی در ربع های مختلف تغییر می کند.
| ربع | I | II | III | IV |
| sinx | + | + | - - | - |
| cosx | + | - | - - | + |
| tanx | + | - | + | - |
| cosecx | + | + | - - | - |
| secx | + | - | - - | + |
| cotx | + | - | + | - |
به جدول زیر نگاه کنید که مقدار زوایای مثلثاتی را برای درجاتی مانند 0 درجه، 30 درجه، 45 درجه، 60 درجه و 90 درجه نشان می دهد.
زوایای (در درجه و رادیان) | sin | cos | tan | cot | csc | sec |
| 0° | 0 | 1 | 0 | ∞ | ∞ | 1 |
| 30° یا π/6 رادیان | 1/2 | √3/2 | 1/√3 | √3 | 2 | 2/√3 |
| 45 ° یا π/4 رادیان | 1/√2 | 1/√2 | 1 | 1 | √2 | √2 |
| 60 درجه یا π/3 رادیان | √3/2 | 1/2 | √3 | 1/ √3 | 2/√3 | 2 |
| 90 درجه یا π/2 رادیان | 1 | 0 | ∞ | 0 | 1 | ∞ |
| 180 درجه یا π رادیان | 0 | -1 | 0 | ∞ | ∞ | -1 |
| 270 درجه یا 3π/2 رادیان | -1 | 0 | ∞ | 0 | - 1 | ∞ |
| 360 درجه یا 2π رادیان | 0 | 1 | 0 | ∞ | ∞ | 1 |
با مشاهده جدول بالا متوجه خواهید شد:
( \mathbf{\tan x = \cot(90^\circ\(\mathbf{\sin x = \cos(90^\circ-x)}\) |
| \(\mathbf{\tan x = \cot(90^\circ-x)}\) |
| \(\mathbf{\tan x = \cot(90^\circ-x)}\) |
| \(\mathbf{\sec x = \csc(90^\circ-x) }\) |
| \(\mathbf{\csc x = \sec(90^\circ-x)}\) |
| \( \mathbf{ \sin(-x) = -\sin x}\) |
| \( \mathbf{ \cos(-x) = \cos x}\) |
| \(\tan(-x) = -\tan x\) |
نمایش گرافیکی \(\sin x\) و \(\cos x\) که در آن y از 1- تا 1+ است زمانی که x مقادیر \(-3\pi \) تا \(3\pi \) را می گیرد. . هر دو مقدار سینوس و کسینوس تابع مثلثاتی پس از فاصله \(2\pi \) تکرار می شوند.
سینوس به صورت خط توپر و کسینوس به صورت نقطه چین نشان داده شده است.
اجازه دهید چند مثال را بر اساس توابع مثلثاتی بالا حل کنیم:
مثال 1: اگر \(\cos x\) = − 4/5، x در ربع سوم قرار دارد، مقادیر پنج تابع مثلثاتی دیگر را پیدا کنید.
راه حل: به جداول بالا مراجعه کنید.
به عنوان \(\cos x\) = -4/5، بنابراین \(\sec x\) = -5/4
به عنوان \(\mathbf{ \cos^2 x + \sin^2x = 1}\) بنابراین \({16\over25} + \sin^2x = 1 ⇒ \sin^2x = 1-\frac{16}{25} = {9\over25}\)
\(\sin x = \pm3/5\)
از آنجایی که x در مقدار ربع سوم قرار دارد، بنابراین \(\sin x\) منفی خواهد بود (به جدول علامت ربع مراجعه کنید). بنابراین \(\sin x\) = -3/5 و \(\csc x \) = -5/3
به عنوان \(\tan x = \sin x/\cos x\) ، بنابراین \(\tan x\) = \(\frac{-4/5}{-3/5}\) = 4/3 مثال
2 : مقدار \(\cos(5\pi/2)\) بیابید
راه حل: \(\cos(5\pi/2) = \cos (2\pi + {1\pi}/_2)\)
وقتی مقدار کسینوس بعد از \(2\pi \) تکرار \(\cos(2\pi + {1\pi}/_2) = \cos(\pi/2) = 0\)