Comme nous savons comment mesurer un angle aigu pour le triangle rectangle en tant que rapport de ses côtés, il est temps d'apprendre les rapports trigonométriques à n'importe quel angle en termes de mesure de radian et de les étudier en tant que fonctions trigonométriques.
Considérons un cercle de rayon unitaire, dont le centre est à l'origine des axes de coordonnées.
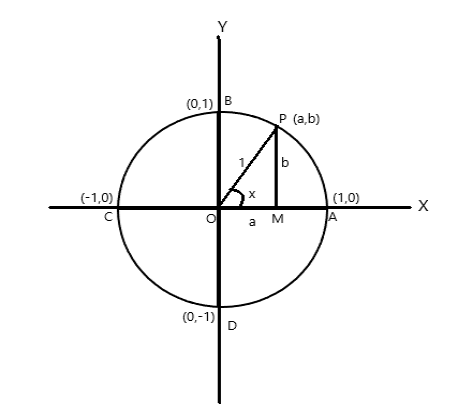
Points de coordonnées de A = (1,0), B = (0,1), C = (-1,0) et D = (0,-1)
Soit P (a,b) un point quelconque du cercle de \(\angle AOP = x \) radian. Donc la longueur de l'arc \(AP = x \) unité.
\(\cos x = a\) , \(\sin x = b\) . Comme \(\bigtriangleup POM\) est un triangle rectangle, \(OP^2 = OM^2 + PM^2\)
donc \(1 = a^2 + b^2\)
| \(\mathbf{ \cos^2 x + \sin^2x = 1}\) |
Puisqu'un tour complet sous-tend au centre du cercle un angle de \(2\pi\) radian. De la figure ci-dessus
\(\angle AOB = \pi/2 \)
\(\angle AOC = \pi\)
\(\angle AOD = \frac{3\pi}{2} \)
Nous savons \(\cos x = \frac {\textrm {Base}}{\textrm{Hypotenuse}}\) et \(\sin x = \frac {\textrm {Perpendicular}}{\textrm{Hypotenuse}}\)
\(\cos0^\circ = 1\) \(\sin0^\circ = 0\)
\(\cos\frac{\pi}{2} = 0\) \(\sin\frac{\pi}{2} = 1\)
\(\cos\pi = -1\) \(\sin\pi = 0\)
\(\cos2\pi = 1\) \(\sin2\pi = 0\)
Lorsque nous prenons une révolution complète à partir du point P, nous atteignons à nouveau le point P. La valeur de \(\cos x\) et \(\sin x\) reste la même, nous pouvons donc dire que
lorsque x augmente ou diminue d'un multiple entier de \(2\pi\) , la valeur de la fonction sinus, cosinus ne change pas. Ainsi,
\(\sin(n\cdot2\pi + x) = \sin x\)
\(\cos(n\cdot 2\pi + x) = \cos x \)
où n est un entier.
On remarquera que \(\sin x = 0\) lorsque \(\space x = n\pi\)
et \(\cos x = 0\) lorsque \(x = (2n+1)\pi/2\)
Dérivation d'autres fonctions trigonométriques en termes de fonctions sinus et cosinus.
| \(\mathbf{\csc x} = \mathbf{\frac{1}{\sin x}}\) où \(x \neq n\pi\) |
| \(\mathbf{\sec x } = \mathbf{\frac{1}{\cos x}}\) où |
| \(\mathbf{\tan x } = \mathbf{\frac{\sin x}{\cos x}}\) où |
| \(\mathbf{\cot x } = \mathbf{\frac{\cos x}{\sin x}}\) où \( x \neq n\pi\) |
| \(\textbf 1 + \mathbf {\tan^2x = \sec^2x}\) |
| \(\textbf 1 + \mathbf {\cot^2x = \csc^2x}\) |
Le tableau ci-dessous montre comment le signe et la valeur des fonctions trigonométriques changent dans différents quadrants.
| Quadrants | je | II | III | IV |
| péché | + | + | − | − |
| cox | + | − | − | + |
| bronzer | + | − | + | − |
| cosecx | + | + | − | − |
| secx | + | − | − | + |
| cox | + | − | + | − |
Jetez un œil au tableau ci-dessous qui montre la valeur des angles trigonométriques pour des degrés tels que 0°, 30°, 45°, 60° et 90°.
Angles (en degrés et radian) | péché | parce que | bronzer | lit bébé | SCC | seconde |
| 0° | 0 | 1 | 0 | ∞ | ∞ | 1 |
| 30° ou π/6 radian | 1/2 | √3/2 | 1/√3 | √3 | 2 | 2/√3 |
| 45° ou π/4 radian | 1/√2 | 1/√2 | 1 | 1 | √2 | √2 |
| 60° ou π/3 radian | √3/2 | 1/2 | √3 | 1/√3 | 2/√3 | 2 |
| 90° ou π/2 radian | 1 | 0 | ∞ | 0 | 1 | ∞ |
| 180° ou π radian | 0 | -1 | 0 | ∞ | ∞ | -1 |
| 270° ou 3π/2 radians | -1 | 0 | ∞ | 0 | -1 | ∞ |
| 360° ou 2π radians | 0 | 1 | 0 | ∞ | ∞ | 1 |
Observez le tableau ci-dessus, vous remarquerez que :
\(\mathbf{\sin x = \cos(90^\circ-x)}\) |
| \(\mathbf{\tan x = \cot(90^\circ-x)}\) |
| \(\mathbf{\sec x = \csc(90^\circ-x) }\) |
| \(\mathbf{\csc x = \sec(90^\circ-x)}\) |
| \( \mathbf{ \sin(-x) = -\sin x}\) |
| \( \mathbf{ \cos(-x) = \cos x}\) |
| \(\tan(-x) = -\tan x\) |
Représentation graphique de \(\sin x\) et \(\cos x\) où y varie de -1 à +1 lorsque x prend des valeurs de \(-3\pi \) à \(3\pi \) . Les valeurs sinus et cosinus de la fonction trigonométrique se répètent après un intervalle de \(2\pi \) .
Le sinus est représenté par une ligne continue et le cosinus par une ligne pointillée.
Résolvons quelques exemples basés sur les fonctions trigonométriques ci-dessus :
Exemple 1 : Si \(\cos x\) = − 4/5, x se trouve dans le troisième quadrant, trouvez les valeurs des cinq autres fonctions trigonométriques.
Solution : Reportez-vous aux tableaux ci-dessus.
Comme \(\cos x\) = -4/5, donc \(\sec x\) = -5/4
Comme \(\mathbf{ \cos^2 x + \sin^2x = 1}\) donc \({16\over25} + \sin^2x = 1 ⇒ \sin^2x = 1-\frac{16}{25} = {9\over25}\)
\(\sin x = \pm3/5\)
Comme x se trouve dans la valeur du troisième quadrant, donc \(\sin x\) sera négatif (reportez-vous au tableau des signes du quadrant). Donc \(\sin x\) = -3/5 et \(\csc x \) = -5/3
Comme \(\tan x = \sin x/\cos x\) , donc \(\tan x\) = \(\frac{-4/5}{-3/5}\) = 4/3
Exemple 2 : Trouver la valeur de \(\cos(5\pi/2)\)
Solution: \(\cos(5\pi/2) = \cos (2\pi + {1\pi}/_2)\)
Comme la valeur du cosinus se répète après \(2\pi \) donc, \(\cos(2\pi + {1\pi}/_2) = \cos(\pi/2) = 0\)