जैसा कि हम जानते हैं कि समकोण त्रिभुज के लिए उसकी भुजाओं के अनुपात के रूप में एक तीव्र कोण को कैसे मापना है, यह रेडियन माप के संदर्भ में किसी भी कोण से त्रिकोणमितीय अनुपात सीखने और त्रिकोणमितीय कार्यों के रूप में उनका अध्ययन करने का समय है।
इकाई त्रिज्या के एक वृत्त पर विचार करें, जिसका केंद्र निर्देशांक अक्षों की उत्पत्ति पर है।
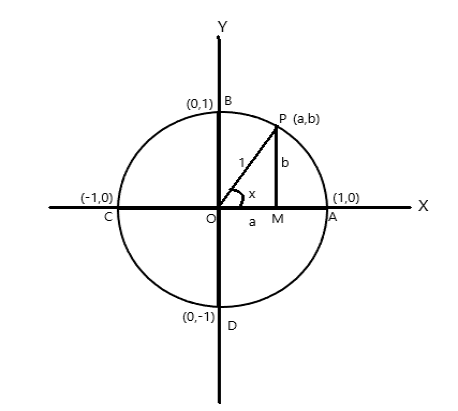
A = (1,0), B = (0,1), C = (-1,0) और D = (0,-1) के निर्देशांक बिंदु
माना \(\angle AOP = x \) रेडियन वाले वृत्त पर P (a,b) कोई बिंदु है। इसलिए चाप की लंबाई \(AP = x \) इकाई।
\(\cos x = a\) , \(\sin x = b\) । चूँकि \(\bigtriangleup POM\) एक समकोण त्रिभुज है, \(OP^2 = OM^2 + PM^2\)
इसलिए \(1 = a^2 + b^2\)
| \(\mathbf{ \cos^2 x + \sin^2x = 1}\) |
चूंकि एक पूर्ण चक्कर वृत्त के केंद्र पर \(2\pi\) रेडियन का कोण बनाता है। उपरोक्त चित्र से
\(\angle AOB = \pi/2 \)
\(\angle AOC = \pi\)
\(\angle AOD = \frac{3\pi}{2} \)
हम जानते हैं \(\cos x = \frac {\textrm {Base}}{\textrm{Hypotenuse}}\) और \(\sin x = \frac {\textrm {Perpendicular}}{\textrm{Hypotenuse}}\)
\(\cos0^\circ = 1\) \(\sin0^\circ = 0\)
\(\cos\frac{\pi}{2} = 0\) \(\sin\frac{\pi}{2} = 1\)
\(\cos\pi = -1\) \(\sin\pi = 0\)
\(\cos2\pi = 1\) \(\sin2\pi = 0\)
जब हम बिंदु P से एक पूर्ण चक्कर लगाते हैं तो हम फिर से बिंदु P पर पहुँच जाते हैं \(\cos x\) और \(\sin x\) का मान समान रहता है, इसलिए हम कह सकते हैं कि
जैसे ही x \(2\pi\) के अभिन्न गुणक से बढ़ता या घटता है, साइन, कोसाइन फ़ंक्शन का मान नहीं बदलता है। इस प्रकार,
\(\sin(n\cdot2\pi + x) = \sin x\)
\(\cos(n\cdot 2\pi + x) = \cos x \)
जहाँ n एक पूर्णांक है।
हम देखेंगे कि \(\sin x = 0\) जब \(\space x = n\pi\)
और \(\cos x = 0\) जब \(x = (2n+1)\pi/2\)
साइन और कोसाइन कार्यों के संदर्भ में अन्य त्रिकोणमितीय कार्यों को प्राप्त करना।
| \(\mathbf{\csc x} = \mathbf{\frac{1}{\sin x}}\) जहाँ \(x \neq n\pi\) |
| \(\mathbf{\sec x } = \mathbf{\frac{1}{\cos x}}\) जहां |
| \(\mathbf{\tan x } = \mathbf{\frac{\sin x}{\cos x}}\) जहां |
| \(\mathbf{\cot x } = \mathbf{\frac{\cos x}{\sin x}}\) जहाँ \( x \neq n\pi\) |
| \(\textbf 1 + \mathbf {\tan^2x = \sec^2x}\) |
| \(\textbf 1 + \mathbf {\cot^2x = \csc^2x}\) |
नीचे दी गई तालिका दर्शाती है कि विभिन्न चतुर्भुजों में त्रिकोणमितीय कार्यों के चिह्न और मान कैसे बदलते हैं।
| चतुर्भाग | मैं | द्वितीय | तृतीय | चतुर्थ |
| sinx | + | + | - | - |
| cosx | + | - | - | + |
| tanx | + | - | + | - |
| cosecx | + | + | - | - |
| secx | + | - | - | + |
| cotx | + | - | + | - |
नीचे दी गई तालिका पर एक नज़र डालें जो 0°, 30°, 45°, 60°, और 90° जैसी डिग्री के लिए त्रिकोणमितीय कोणों का मान दर्शाती है।
कोण (डिग्री और रेडियन में) | पाप | ओल | टैन | खाट | सीएससी | सेकंड |
| 0 डिग्री | 0 | 1 | 0 | ∞ | ∞ | 1 |
| 30° या π/6 रेडियन | 1/2 | √3/2 | 1/√3 | √3 | 2 | 2/√3 |
| 45° या π/4 रेडियन | 1/√2 | 1/√2 | 1 | 1 | √2 | √2 |
| 60° या π/3 रेडियन | √3/2 | 1/2 | √3 | 1/√3 | 2/√3 | 2 |
| 90° या π/2 रेडियन | 1 | 0 | ∞ | 0 | 1 | ∞ |
| 180° या π रेडियन | 0 | -1 | 0 | ∞ | ∞ | -1 |
| 270 डिग्री या 3π/2 रेडियन | -1 | 0 | ∞ | 0 | -1 | ∞ |
| 360° या 2π रेडियन | 0 | 1 | 0 | ∞ | ∞ | 1 |
उपरोक्त तालिका का अवलोकन करें, आप देखेंगे कि:
\(\mathbf{\sin x = \cos(90^\circ-x)}\) |
| \(\mathbf{\tan x = \cot(90^\circ-x)}\) |
| \(\mathbf{\sec x = \csc(90^\circ-x) }\) |
| \(\mathbf{\csc x = \sec(90^\circ-x)}\) |
| \( \mathbf{ \sin(-x) = -\sin x}\) |
| \( \mathbf{ \cos(-x) = \cos x}\) |
| \(\tan(-x) = -\tan x\) |
\(\sin x\) और \(\cos x\) का ग्राफिकल प्रतिनिधित्व जहां y -1 से +1 तक होता है जब x \(-3\pi \) से \(3\pi \) तक मान लेता है। त्रिकोणमितीय फलन sine और cosine दोनों के मान \(2\pi \) के अंतराल के बाद दोहराते हैं।
साइन को एक ठोस रेखा के रूप में और कोसाइन को बिंदीदार रेखा के रूप में दिखाया गया है।
आइए उपरोक्त त्रिकोणमितीय कार्यों के आधार पर कुछ उदाहरण हल करें:
उदाहरण 1: यदि \(\cos x\) = - 4/5, x तीसरे चतुर्थांश में स्थित है, तो अन्य पांच त्रिकोणमितीय कार्यों के मान ज्ञात कीजिए।
हलः ऊपर दी गई तालिका देखें।
चूंकि \(\cos x\) = -4/5, इसलिए \(\sec x\) = -5/4
\(\mathbf{ \cos^2 x + \sin^2x = 1}\) तो \({16\over25} + \sin^2x = 1 ⇒ \sin^2x = 1-\frac{16}{25} = {9\over25}\)
\(\sin x = \pm3/5\)
चूँकि x तृतीय चतुर्थांश मान में निहित है, इसलिए \(\sin x\) ऋणात्मक होगा (चतुर्भुज चिह्न तालिका देखें)। इसलिए \(\sin x\) = -3/5 और \(\csc x \) = -5/3
चूंकि \(\tan x = \sin x/\cos x\) , इसलिए \(\tan x\) = \(\frac{-4/5}{-3/5}\) = 4/3
उदाहरण 2: \(\cos(5\pi/2)\) का मान ज्ञात कीजिए
समाधान: \(\cos(5\pi/2) = \cos (2\pi + {1\pi}/_2)\)
\(2\pi \) के बाद कोसाइन का मान दोहराता है, इसलिए \(\cos(2\pi + {1\pi}/_2) = \cos(\pi/2) = 0\)