Kako znamo izmjeriti šiljasti kut za pravokutni trokut kao omjer njegovih stranica, vrijeme je da naučimo trigonometrijske omjere prema bilo kojem kutu u smislu mjere radijana i proučavamo ih kao trigonometrijske funkcije.
Promotrimo krug jediničnog radijusa čije je središte u ishodištu koordinatnih osi.
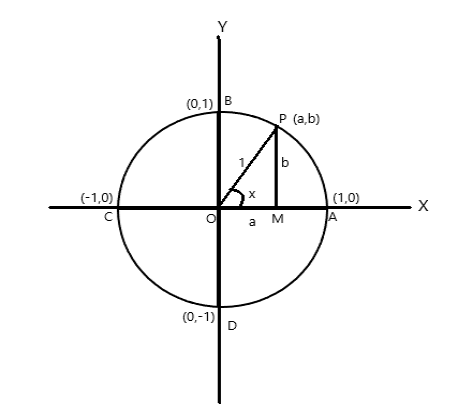
Koordinatne točke A = (1,0), B = (0,1), C = (-1,0) i D = (0,-1)
Neka je P (a,b) bilo koja točka na kružnici s \(\angle AOP = x \) radijana. Stoga je duljina luka \(AP = x \) jedinica.
\(\cos x = a\) , \(\sin x = b\) . Kako je \(\bigtriangleup POM\) pravokutni trokut, \(OP^2 = OM^2 + PM^2\)
dakle \(1 = a^2 + b^2\)
| \(\mathbf{ \cos^2 x + \sin^2x = 1}\) |
Budući da jedan potpuni okret u središtu kruga zatvara kut od \(2\pi\) radijana. Iz gornje slike
\(\angle AOB = \pi/2 \)
\(\angle AOC = \pi\)
\(\angle AOD = \frac{3\pi}{2} \)
Znamo \(\cos x = \frac {\textrm {Base}}{\textrm{Hypotenuse}}\) i \(\sin x = \frac {\textrm {Perpendicular}}{\textrm{Hypotenuse}}\)
\(\cos0^\circ = 1\) \(\sin0^\circ = 0\)
\(\cos\frac{\pi}{2} = 0\) \(\sin\frac{\pi}{2} = 1\)
\(\cos\pi = -1\) \(\sin\pi = 0\)
\(\cos2\pi = 1\) \(\sin2\pi = 0\)
Kad napravimo jedan puni krug od točke P, ponovno dolazimo do točke P. Vrijednost \(\cos x\) i \(\sin x\) ostaje ista, stoga možemo reći da
kako se x povećava ili smanjuje za integralni višekratnik \(2\pi\) , vrijednost sinusne, kosinusne funkcije se ne mijenja. Tako,
\(\sin(n\cdot2\pi + x) = \sin x\)
\(\cos(n\cdot 2\pi + x) = \cos x \)
gdje je n cijeli broj.
Primijetit ćemo da \(\sin x = 0\) kada \(\space x = n\pi\)
i \(\cos x = 0\) kada je \(x = (2n+1)\pi/2\)
Izvođenje drugih trigonometrijskih funkcija u terminima sinusne i kosinusne funkcije.
| \(\mathbf{\csc x} = \mathbf{\frac{1}{\sin x}}\) gdje je \(x \neq n\pi\) |
| \(\mathbf{\sec x } = \mathbf{\frac{1}{\cos x}}\) gdje |
| \(\mathbf{\tan x } = \mathbf{\frac{\sin x}{\cos x}}\) gdje |
| \(\mathbf{\cot x } = \mathbf{\frac{\cos x}{\sin x}}\) gdje je \( x \neq n\pi\) |
| \(\textbf 1 + \mathbf {\tan^2x = \sec^2x}\) |
| \(\textbf 1 + \mathbf {\cot^2x = \csc^2x}\) |
Donja tablica pokazuje kako se predznak i vrijednost trigonometrijskih funkcija mijenjaju u različitim kvadrantima.
| Kvadranti | ja | II | III | IV |
| sinx | + | + | − | − |
| cosx | + | − | − | + |
| Tanx | + | − | + | − |
| cosecx | + | + | − | − |
| secx | + | − | − | + |
| cotx | + | − | + | − |
Pogledajte donju tablicu koja prikazuje vrijednost trigonometrijskih kutova za stupnjeve kao što su 0°, 30°, 45°, 60° i 90°.
Kutovi (u stupnjevima i radijanima) | grijeh | cos | preplanuli ten | dječji krevetić | csc | sek |
| 0° | 0 | 1 | 0 | ∞ | ∞ | 1 |
| 30° ili π/6 radijana | 1/2 | √3/2 | 1/√3 | √3 | 2 | 2/√3 |
| 45° ili π/4 radijana | 1/√2 | 1/√2 | 1 | 1 | √2 | √2 |
| 60° ili π/3 radijana | √3/2 | 1/2 | √3 | 1/√3 | 2/√3 | 2 |
| 90° ili π/2 radijana | 1 | 0 | ∞ | 0 | 1 | ∞ |
| 180° ili π radijana | 0 | -1 | 0 | ∞ | ∞ | -1 |
| 270° ili 3π/2 radijana | -1 | 0 | ∞ | 0 | -1 | ∞ |
| 360° ili 2π radijana | 0 | 1 | 0 | ∞ | ∞ | 1 |
Promatrajte gornju tablicu, primijetit ćete da:
\(\mathbf{\sin x = \cos(90^\circ-x)}\) |
| \(\mathbf{\tan x = \cot(90^\circ-x)}\) |
| \(\mathbf{\sec x = \csc(90^\circ-x) }\) |
| \(\mathbf{\csc x = \sec(90^\circ-x)}\) |
| \( \mathbf{ \sin(-x) = -\sin x}\) |
| \( \mathbf{ \cos(-x) = \cos x}\) |
| \(\tan(-x) = -\tan x\) |
Grafički prikaz \(\sin x\) i \(\cos x\) gdje je y u rasponu od -1 do +1 kada x ima vrijednosti od \(-3\pi \) do \(3\pi \) . Vrijednosti sinusa i kosinusa trigonometrijske funkcije ponavljaju se nakon intervala od \(2\pi \) .
Sinus je prikazan kao puna linija, a kosinus kao isprekidana linija.
Riješimo nekoliko primjera na temelju gornjih trigonometrijskih funkcija:
Primjer 1: Ako je \(\cos x\) = − 4/5, x leži u trećem kvadrantu, pronađite vrijednosti ostalih pet trigonometrijskih funkcija.
Rješenje: pogledajte gornje tablice.
Kako je \(\cos x\) = -4/5, dakle \(\sec x\) = -5/4
Kao što \(\mathbf{ \cos^2 x + \sin^2x = 1}\) tako \({16\over25} + \sin^2x = 1 ⇒ \sin^2x = 1-\frac{16}{25} = {9\over25}\)
\(\sin x = \pm3/5\)
Kako x leži u vrijednosti trećeg kvadranta, tako će \(\sin x\) biti negativan (pogledajte tablicu predznaka kvadranta). Prema tome \(\sin x\) = -3/5 i \(\csc x \) = -5/3
Kako je \(\tan x = \sin x/\cos x\) , dakle \(\tan x\) = \(\frac{-4/5}{-3/5}\) = 4/3
Primjer 2: Pronađite vrijednost \(\cos(5\pi/2)\)
Riješenje: \(\cos(5\pi/2) = \cos (2\pi + {1\pi}/_2)\)
Kako se vrijednost kosinusa ponavlja nakon \(2\pi \) , dakle \(\cos(2\pi + {1\pi}/_2) = \cos(\pi/2) = 0\)