Seperti yang kita ketahui bagaimana mengukur sudut lancip untuk segitiga siku-siku sebagai perbandingan sisi-sisinya, sekarang saatnya mempelajari perbandingan trigonometri dengan sudut manapun dalam satuan radian dan mempelajarinya sebagai fungsi trigonometri.
Pertimbangkan lingkaran jari-jari satuan, yang pusatnya berada di asal sumbu koordinat.
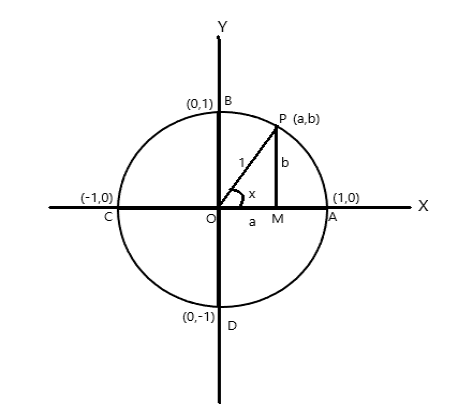
Titik koordinat A = (1,0), B = (0,1), C = (-1,0) dan D = (0,-1)
Misalkan P (a,b) sembarang titik pada lingkaran dengan \(\angle AOP = x \) radian. Oleh karena itu panjang busur \(AP = x \) satuan.
\(\cos x = a\) , \(\sin x = b\) . Karena \(\bigtriangleup POM\) adalah segitiga siku-siku, \(OP^2 = OM^2 + PM^2\)
oleh karena itu \(1 = a^2 + b^2\)
| \(\mathbf{ \cos^2 x + \sin^2x = 1}\) |
Karena satu putaran penuh membentuk sudut \(2\pi\) radian di pusat lingkaran. Dari gambar di atas
\(\angle AOB = \pi/2 \)
\(\angle AOC = \pi\)
\(\angle AOD = \frac{3\pi}{2} \)
Kita tahu \(\cos x = \frac {\textrm {Base}}{\textrm{Hypotenuse}}\) dan \(\sin x = \frac {\textrm {Perpendicular}}{\textrm{Hypotenuse}}\)
\(\cos0^\circ = 1\) \(\sin0^\circ = 0\)
\(\cos\frac{\pi}{2} = 0\) \(\sin\frac{\pi}{2} = 1\)
\(\cos\pi = -1\) \(\sin\pi = 0\)
\(\cos2\pi = 1\) \(\sin2\pi = 0\)
Saat kita mengambil satu putaran penuh dari titik P kita kembali mencapai titik P. Nilai \(\cos x\) dan \(\sin x\) tetap sama, maka kita dapat mengatakan bahwa
saat x bertambah atau berkurang dengan kelipatan integral \(2\pi\) , nilai fungsi sinus, cosinus tidak berubah. Dengan demikian,
\(\sin(n\cdot2\pi + x) = \sin x\)
\(\cos(n\cdot 2\pi + x) = \cos x \)
di mana n adalah bilangan bulat.
Kita akan melihat bahwa \(\sin x = 0\) ketika \(\space x = n\pi\)
dan \(\cos x = 0\) ketika \(x = (2n+1)\pi/2\)
Turunkan fungsi trigonometri lainnya dalam bentuk fungsi sinus dan cosinus.
| \(\mathbf{\csc x} = \mathbf{\frac{1}{\sin x}}\) di mana \(x \neq n\pi\) |
| \(\mathbf{\sec x } = \mathbf{\frac{1}{\cos x}}\) di mana |
| \(\mathbf{\tan x } = \mathbf{\frac{\sin x}{\cos x}}\) di mana |
| \(\mathbf{\cot x } = \mathbf{\frac{\cos x}{\sin x}}\) di mana \( x \neq n\pi\) |
| \(\textbf 1 + \mathbf {\tan^2x = \sec^2x}\) |
| \(\textbf 1 + \mathbf {\cot^2x = \csc^2x}\) |
Tabel di bawah ini menunjukkan bagaimana tanda dan nilai fungsi trigonometri berubah di kuadran yang berbeda.
| Kuadran | SAYA | II | AKU AKU AKU | IV |
| sinx | + | + | − | − |
| cosx | + | − | − | + |
| tanx | + | − | + | − |
| cosecx | + | + | − | − |
| sexx | + | − | − | + |
| cotx | + | − | + | − |
Perhatikan tabel di bawah ini yang menunjukkan nilai sudut trigonometri untuk derajat seperti 0°, 30°, 45°, 60°, dan 90°.
Sudut (dalam derajat & radian) | dosa | cos | cokelat | pondok | csc | detik |
| 0° | 0 | 1 | 0 | ∞ | ∞ | 1 |
| 30° atau π/6 radian | 1/2 | √3/2 | 1/√3 | √3 | 2 | 2/√3 |
| 45° atau π/4 radian | 1/√2 | 1/√2 | 1 | 1 | √2 | √2 |
| 60° atau π/3 radian | √3/2 | 1/2 | √3 | 1/√3 | 2/√3 | 2 |
| 90° atau π/2 radian | 1 | 0 | ∞ | 0 | 1 | ∞ |
| 180° atau π radian | 0 | -1 | 0 | ∞ | ∞ | -1 |
| 270° atau 3π/2 radian | -1 | 0 | ∞ | 0 | -1 | ∞ |
| 360° atau 2π radian | 0 | 1 | 0 | ∞ | ∞ | 1 |
Perhatikan tabel di atas, Anda akan melihat bahwa:
\(\mathbf{\sin x = \cos(90^\circ-x)}\) |
| \(\mathbf{\tan x = \cot(90^\circ-x)}\) |
| \(\mathbf{\sec x = \csc(90^\circ-x) }\) |
| \(\mathbf{\csc x = \sec(90^\circ-x)}\) |
| \( \mathbf{ \sin(-x) = -\sin x}\) |
| \( \mathbf{ \cos(-x) = \cos x}\) |
| \(\tan(-x) = -\tan x\) |
Representasi grafis dari \(\sin x\) dan \(\cos x\) di mana y berkisar dari -1 hingga +1 saat x mengambil nilai dari \(-3\pi \) hingga \(3\pi \) . Baik nilai sinus dan cosinus fungsi trigonometri berulang setelah selang waktu \(2\pi \) .
Sinus ditampilkan sebagai garis padat dan Cosinus sebagai garis putus-putus.
Mari kita pecahkan beberapa contoh berdasarkan fungsi trigonometri di atas:
Contoh 1: Jika \(\cos x\) = − 4/5, x terletak di kuadran ketiga, carilah nilai dari lima fungsi trigonometri lainnya.
Solusi: Lihat tabel yang diberikan di atas.
Karena \(\cos x\) = -4/5, maka \(\sec x\) = -5/4
Sebagai \(\mathbf{ \cos^2 x + \sin^2x = 1}\) jadi \({16\over25} + \sin^2x = 1 ⇒ \sin^2x = 1-\frac{16}{25} = {9\over25}\)
\(\sin x = \pm3/5\)
Karena x terletak pada nilai kuadran ketiga, maka \(\sin x\) akan negatif (lihat tabel tanda kuadran). Oleh karena itu \(\sin x\) = -3/5 dan \(\csc x \) = -5/3
Sebagai \(\tan x = \sin x/\cos x\) , maka \(\tan x\) = \(\frac{-4/5}{-3/5}\) = 4/3
Contoh 2: Temukan nilai dari \(\cos(5\pi/2)\)
Larutan: \(\cos(5\pi/2) = \cos (2\pi + {1\pi}/_2)\)
Karena nilai cosinus berulang setelah \(2\pi \) maka, \(\cos(2\pi + {1\pi}/_2) = \cos(\pi/2) = 0\)