Poiché sappiamo come misurare un angolo acuto per il triangolo rettangolo come rapporto tra i suoi lati, è tempo di imparare i rapporti trigonometrici a qualsiasi angolo in termini di misura in radianti e studiarli come funzioni trigonometriche.
Considera un cerchio di raggio unitario, il cui centro è all'origine degli assi delle coordinate.
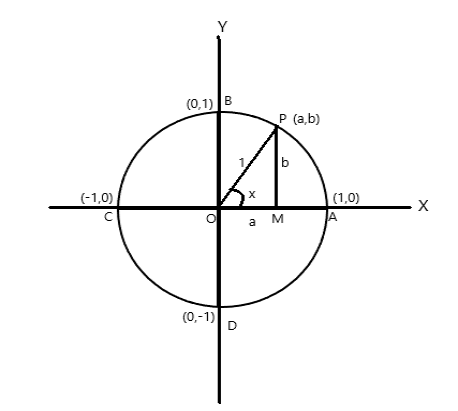
Punti di coordinate di A = (1,0), B = (0,1), C = (-1,0) e D = (0,-1)
Sia P (a,b) un qualsiasi punto della circonferenza con \(\angle AOP = x \) radianti. Pertanto la lunghezza dell'arco \(AP = x \) unità.
\(\cos x = a\) , \(\sin x = b\) . Poiché \(\bigtriangleup POM\) è un triangolo rettangolo, \(OP^2 = OM^2 + PM^2\)
quindi \(1 = a^2 + b^2\)
| \(\mathbf{ \cos^2 x + \sin^2x = 1}\) |
Poiché un giro completo sottende al centro del cerchio un angolo di \(2\pi\) radianti. Dalla figura sopra
\(\angle AOB = \pi/2 \)
\(\angle AOC = \pi\)
\(\angle AOD = \frac{3\pi}{2} \)
Sappiamo \(\cos x = \frac {\textrm {Base}}{\textrm{Hypotenuse}}\) e \(\sin x = \frac {\textrm {Perpendicular}}{\textrm{Hypotenuse}}\)
\(\cos0^\circ = 1\) \(\sin0^\circ = 0\)
\(\cos\frac{\pi}{2} = 0\) \(\sin\frac{\pi}{2} = 1\)
\(\cos\pi = -1\) \(\sin\pi = 0\)
\(\cos2\pi = 1\) \(\sin2\pi = 0\)
Facendo un giro completo dal punto P raggiungiamo nuovamente il punto P. Il valore di \(\cos x\) e \(\sin x\) rimane lo stesso, quindi possiamo dire che
quando x aumenta o diminuisce di un multiplo intero di \(2\pi\) , il valore della funzione seno, coseno non cambia. Così,
\(\sin(n\cdot2\pi + x) = \sin x\)
\(\cos(n\cdot 2\pi + x) = \cos x \)
dove n è un numero intero.
Noteremo che \(\sin x = 0\) quando \(\space x = n\pi\)
e \(\cos x = 0\) quando \(x = (2n+1)\pi/2\)
Derivazione di altre funzioni trigonometriche in termini di funzioni seno e coseno.
| \(\mathbf{\csc x} = \mathbf{\frac{1}{\sin x}}\) dove \(x \neq n\pi\) |
| \(\mathbf{\sec x } = \mathbf{\frac{1}{\cos x}}\) dove |
| \(\mathbf{\tan x } = \mathbf{\frac{\sin x}{\cos x}}\) dove |
| \(\mathbf{\cot x } = \mathbf{\frac{\cos x}{\sin x}}\) dove \( x \neq n\pi\) |
| \(\textbf 1 + \mathbf {\tan^2x = \sec^2x}\) |
| \(\textbf 1 + \mathbf {\cot^2x = \csc^2x}\) |
La tabella sottostante mostra come il segno e il valore delle funzioni trigonometriche cambiano nei diversi quadranti.
| Quadranti | IO | II | III | IV |
| sinx | + | + | − | − |
| cosx | + | − | − | + |
| tanx | + | − | + | − |
| cosecx | + | + | − | − |
| secx | + | − | − | + |
| cox | + | − | + | − |
Dai un'occhiata alla tabella sottostante che mostra il valore degli angoli trigonometrici per gradi come 0°, 30°, 45°, 60° e 90°.
Angoli (in gradi e radianti) | peccato | cos | abbronzatura | culla | csc | sec |
| 0° | 0 | 1 | 0 | ∞ | ∞ | 1 |
| 30° o π/6 radianti | 1/2 | √3/2 | 1/√3 | √3 | 2 | 2/√3 |
| 45° o π/4 radianti | 1/√2 | 1/√2 | 1 | 1 | √2 | √2 |
| 60° o π/3 radianti | √3/2 | 1/2 | √3 | 1/√3 | 2/√3 | 2 |
| 90° o π/2 radianti | 1 | 0 | ∞ | 0 | 1 | ∞ |
| 180° o π radianti | 0 | -1 | 0 | ∞ | ∞ | -1 |
| 270° o 3π/2 radianti | -1 | 0 | ∞ | 0 | -1 | ∞ |
| 360° o 2π radianti | 0 | 1 | 0 | ∞ | ∞ | 1 |
Osserva la tabella sopra, noterai che:
\(\mathbf{\sin x = \cos(90^\circ-x)}\) |
| \(\mathbf{\tan x = \cot(90^\circ-x)}\) |
| \(\mathbf{\sec x = \csc(90^\circ-x) }\) |
| \(\mathbf{\csc x = \sec(90^\circ-x)}\) |
| \( \mathbf{ \sin(-x) = -\sin x}\) |
| \( \mathbf{ \cos(-x) = \cos x}\) |
| \(\tan(-x) = -\tan x\) |
Rappresentazione grafica di \(\sin x\) e \(\cos x\) dove y varia da -1 a +1 quando x assume valori da \(-3\pi \) a \(3\pi \) . Entrambi i valori della funzione trigonometrica seno e coseno si ripetono dopo un intervallo di \(2\pi \) .
Il seno è mostrato come una linea continua e il coseno come una linea tratteggiata.
Risolviamo alcuni esempi basati sulle funzioni trigonometriche di cui sopra:
Esempio 1: Se \(\cos x\) = − 4/5, x si trova nel terzo quadrante, trovare i valori delle altre cinque funzioni trigonometriche.
Soluzione: fare riferimento alle tabelle sopra riportate.
Poiché \(\cos x\) = -4/5, allora \(\sec x\) = -5/4
Poiché \(\mathbf{ \cos^2 x + \sin^2x = 1}\) allora \({16\over25} + \sin^2x = 1 ⇒ \sin^2x = 1-\frac{16}{25} = {9\over25}\)
\(\sin x = \pm3/5\)
Poiché x si trova nel valore del terzo quadrante, \(\sin x\) sarà negativo (fare riferimento alla tabella dei segni del quadrante). Pertanto \(\sin x\) = -3/5 e \(\csc x \) = -5/3
Poiché \(\tan x = \sin x/\cos x\) , quindi \(\tan x\) = \(\frac{-4/5}{-3/5}\) = 4/3
Esempio 2: trovare il valore di \(\cos(5\pi/2)\)
Soluzione: \(\cos(5\pi/2) = \cos (2\pi + {1\pi}/_2)\)
Poiché il valore del coseno si ripete dopo \(2\pi \) quindi, \(\cos(2\pi + {1\pi}/_2) = \cos(\pi/2) = 0\)