直角三角形の鋭角を辺の比として測定する方法がわかったので、ラジアン単位で任意の角度に対する三角比を学習し、三角関数として学習します。
中心が座標軸の原点にある単位半径の円を考えます。
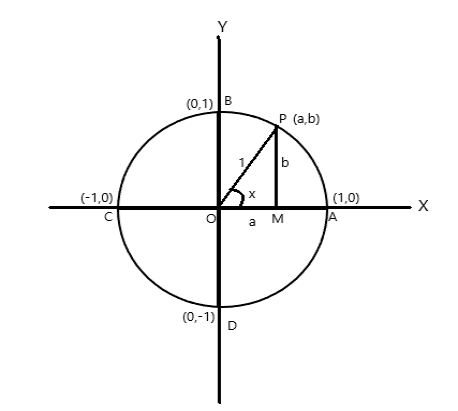
A = (1,0)、B = (0,1)、C = (-1,0)、D = (0,-1) の座標点
P (a,b) を\(\angle AOP = x \)ラジアンの円上の任意の点とします。したがって、円弧の長さは\(AP = x \)単位になります。
\(\cos x = a\) 、 \(\sin x = b\) 。 \(\bigtriangleup POM\)直角三角形なので、 \(OP^2 = OM^2 + PM^2\)
したがって\(1 = a^2 + b^2\)
| \(\mathbf{ \cos^2 x + \sin^2x = 1}\) |
完全な 1 回転は円の中心に収まるので、角度は\(2\pi\)ラジアンになります。上図より
\(\angle AOB = \pi/2 \)
\(\angle AOC = \pi\)
\(\angle AOD = \frac{3\pi}{2} \)
\(\cos x = \frac {\textrm {Base}}{\textrm{Hypotenuse}}\) \(\sin x = \frac {\textrm {Perpendicular}}{\textrm{Hypotenuse}}\)わかっています\(\sin x = \frac {\textrm {Perpendicular}}{\textrm{Hypotenuse}}\)
\(\cos0^\circ = 1\) \(\sin0^\circ = 0\)
\(\cos\frac{\pi}{2} = 0\) \(\sin\frac{\pi}{2} = 1\)
\(\cos\pi = -1\) \(\sin\pi = 0\)
\(\cos2\pi = 1\) \(\sin2\pi = 0\)
点 P から 1 回転すると、再び点 P に到達します\(\cos x\)と\(\sin x\)の値は変わらないため、次のように言えます。
x が\(2\pi\)の整数倍だけ増減しても、サイン関数、コサイン関数の値は変わりません。したがって、
\(\sin(n\cdot2\pi + x) = \sin x\)
\(\cos(n\cdot 2\pi + x) = \cos x \)
ここで、n は整数です。
\(\space x = n\pi\)のとき\(\sin x = 0\)であることがわかります。
\(\cos x = 0\) \(x = (2n+1)\pi/2\)の場合、\(\cos x = 0\)
サイン関数とコサイン関数に関する他の三角関数の導出。
| \(\mathbf{\csc x} = \mathbf{\frac{1}{\sin x}}\)ここで\(x \neq n\pi\) |
| \(\mathbf{\sec x } = \mathbf{\frac{1}{\cos x}}\)ここで |
| \(\mathbf{\tan x } = \mathbf{\frac{\sin x}{\cos x}}\)ここで |
| \(\mathbf{\cot x } = \mathbf{\frac{\cos x}{\sin x}}\)ここで\( x \neq n\pi\) |
| \(\textbf 1 + \mathbf {\tan^2x = \sec^2x}\) |
| \(\textbf 1 + \mathbf {\cot^2x = \csc^2x}\) |
以下の表は、三角関数の符号と値が象限ごとにどのように変化するかを示しています。
| 象限 | 私 | Ⅱ | Ⅲ | Ⅳ |
| シンクス | + | + | − | − |
| コックス | + | − | − | + |
| タンクス | + | − | + | − |
| コセク | + | + | − | − |
| セックス | + | − | − | + |
| コットス | + | − | + | − |
0°、30°、45°、60°、90°などの度ごとの三角関数の角度の値を示す以下の表をご覧ください。
角度(度およびラジアン) | 罪 | コス | 黄褐色 | ベビーベッド | csc | 秒 |
| 0° | 0 | 1 | 0 | ∞ | ∞ | 1 |
| 30°またはπ/6ラジアン | 1/2 | √3/2 | 1/√3 | √3 | 2 | 2/√3 |
| 45°またはπ/4ラジアン | 1/√2 | 1/√2 | 1 | 1 | √2 | √2 |
| 60°またはπ/3ラジアン | √3/2 | 1/2 | √3 | 1/√3 | 2/√3 | 2 |
| 90°またはπ/2ラジアン | 1 | 0 | ∞ | 0 | 1 | ∞ |
| 180°またはπラジアン | 0 | -1 | 0 | ∞ | ∞ | -1 |
| 270°または3π/2ラジアン | -1 | 0 | ∞ | 0 | -1 | ∞ |
| 360°または2πラジアン | 0 | 1 | 0 | ∞ | ∞ | 1 |
上の表を観察すると、次のことがわかります。
\(\mathbf{\sin x = \cos(90^\circ-x)}\) |
| \(\mathbf{\tan x = \cot(90^\circ-x)}\) |
| \(\mathbf{\sec x = \csc(90^\circ-x) }\) |
| \(\mathbf{\csc x = \sec(90^\circ-x)}\) |
| \( \mathbf{ \sin(-x) = -\sin x}\) |
| \( \mathbf{ \cos(-x) = \cos x}\) |
| \(\tan(-x) = -\tan x\) |
\(\sin x\)と\(\cos x\)のグラフ表現。 x が\(-3\pi \)から\(3\pi \)までの値を取るとき、 y は -1 から +1 の範囲になります。三角関数のサイン値とコサイン値は両方とも\(2\pi \)の間隔の後に繰り返されます。
サインは実線で示され、コサインは点線で示されます。
上記の三角関数に基づいていくつかの例を解いてみましょう。
例 1: \(\cos x\) = − 4/5、x が第 3 象限にある場合、他の 5 つの三角関数の値を求めます。
解決策: 上記の表を参照してください。
\(\cos x\) = -4/5 なので、 \(\sec x\) = -5/4
\(\mathbf{ \cos^2 x + \sin^2x = 1}\)なので\({16\over25} + \sin^2x = 1 ⇒ \sin^2x = 1-\frac{16}{25} = {9\over25}\)
\(\sin x = \pm3/5\)
x は第 3 象限の値にあるため、 \(\sin x\)は負になります (象限の符号表を参照)。したがって、 \(\sin x\) = -3/5 および\(\csc x \) = -5/3
\(\tan x = \sin x/\cos x\)なので、 \(\tan x\) = \(\frac{-4/5}{-3/5}\) = 4/3
例 2: \(\cos(5\pi/2)\)の値を求める
解決: \(\cos(5\pi/2) = \cos (2\pi + {1\pi}/_2)\)
コサインの値は\(2\pi \) \(\cos(2\pi + {1\pi}/_2) = \cos(\pi/2) = 0\)