Бидејќи знаеме како да мериме остар агол за правоаголниот триаголник како однос на неговите страни, време е да ги научиме тригонометриските соодноси на кој било агол во однос на радијанската мерка и да ги проучуваме како тригонометриски функции.
Размислете за круг со единица радиус, чиј центар е на почетокот на координатните оски.
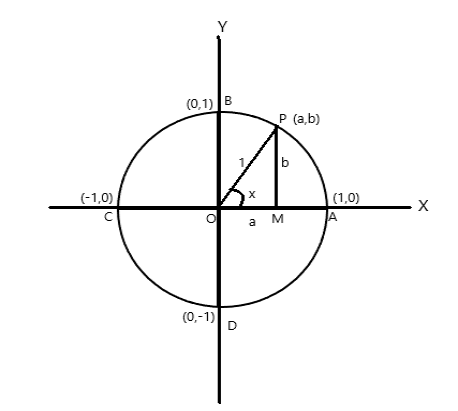
Координатни точки од A = (1,0), B = (0,1), C = (-1,0) и D = (0,-1)
Нека P (a,b) е која било точка на кругот со \(\angle AOP = x \) радијан. Затоа должината на лакот \(AP = x \) единица.
\(\cos x = a\) , \(\sin x = b\) . Бидејќи \(\bigtriangleup POM\) е правоаголен триаголник, \(OP^2 = OM^2 + PM^2\)
затоа \(1 = a^2 + b^2\)
| \(\mathbf{ \cos^2 x + \sin^2x = 1}\) |
Со оглед на тоа што една целосна револуција се подвига во центарот на кругот агол од \(2\pi\) радијан. Од горната слика
\(\angle AOB = \pi/2 \)
\(\angle AOC = \pi\)
\(\angle AOD = \frac{3\pi}{2} \)
Знаеме \(\cos x = \frac {\textrm {Base}}{\textrm{Hypotenuse}}\) и \(\sin x = \frac {\textrm {Perpendicular}}{\textrm{Hypotenuse}}\)
\(\cos0^\circ = 1\) \(\sin0^\circ = 0\)
\(\cos\frac{\pi}{2} = 0\) \(\sin\frac{\pi}{2} = 1\)
\(\cos\pi = -1\) \(\sin\pi = 0\)
\(\cos2\pi = 1\) \(\sin2\pi = 0\)
Кога земаме една целосна револуција од точката P, повторно доаѓаме до точката P. Вредноста на \(\cos x\) и \(\sin x\) останува иста, па оттука можеме да кажеме дека
како што x се зголемува или намалува за интегрален множител на \(2\pi\) , вредноста на синус, косинус функција не се менува. Така,
\(\sin(n\cdot2\pi + x) = \sin x\)
\(\cos(n\cdot 2\pi + x) = \cos x \)
каде n е цел број.
Ќе забележиме дека \(\sin x = 0\) кога \(\space x = n\pi\)
и \(\cos x = 0\) кога \(x = (2n+1)\pi/2\)
Изведување на други тригонометриски функции во однос на синусните и косинусните функции.
| \(\mathbf{\csc x} = \mathbf{\frac{1}{\sin x}}\) каде \(x \neq n\pi\) |
| \(\mathbf{\sec x } = \mathbf{\frac{1}{\cos x}}\) каде што |
| \(\mathbf{\tan x } = \mathbf{\frac{\sin x}{\cos x}}\) каде што |
| \(\mathbf{\cot x } = \mathbf{\frac{\cos x}{\sin x}}\) каде \( x \neq n\pi\) |
| \(\textbf 1 + \mathbf {\tan^2x = \sec^2x}\) |
| \(\textbf 1 + \mathbf {\cot^2x = \csc^2x}\) |
Табелата подолу покажува како знакот и вредноста на тригонометриските функции се менуваат во различни квадранти.
| Квадранти | I | II | III | IV |
| sinx | + | + | − | − |
| cosx | + | − | − | + |
| tanx | + | − | + | − |
| cosecx | + | + | − | − |
| secx | + | − | − | + |
| cotx | + | − | + | − |
Погледнете ја табелата подолу која ја покажува вредноста на тригонометриските агли за степени како што се 0°, 30°, 45°, 60° и 90°.
Агли (во степени и радијани) | sin | cos | tan | cot | csc | sec |
| 0° | 0 | 1 | 0 | ∞ | ∞ | 1 |
| 30° или π/6 радијани | 1/2 | √3/2 | 1/√3 | √3 | 2 | 2/√3 |
| 45 ° или π/4 радијани | 1/√2 | 1/√2 | 1 | 1 | √2 | √2 |
| 60° или π/3 радијани | √3/2 | 1/2 | √3 | 1/ √3 | 2/√3 | 2 |
| 90° или π/2 радијан | 1 | 0 | ∞ | 0 | 1 | ∞ |
| 180° или π радијан | 0 | -1 | 0 | ∞ | ∞ | -1 |
| 270° или 3π/2 радијан | -1 | 0 | ∞ | 0 | - 1 | ∞ |
| 360° или 2π радијан | 0 | 1 | 0 | ∞ | ∞ | 1 |
Набљудувајте ја горната табела, ќе забележите дека:
( \mathbf{\tan x = \cot(90^\circ\(\mathbf{\sin x = \cos(90^\circ-x)}\) |
| \(\mathbf{\tan x = \cot(90^\circ-x)}\) |
| \(\mathbf{\tan x = \cot(90^\circ-x)}\) |
| \(\mathbf{\sec x = \csc(90^\circ-x) }\) |
| \(\mathbf{\csc x = \sec(90^\circ-x)}\) |
| \( \mathbf{ \sin(-x) = -\sin x}\) |
| \( \mathbf{ \cos(-x) = \cos x}\) |
| \(\tan(-x) = -\tan x\) |
Графички приказ на \(\sin x\) и \(\cos x\) каде што y се движи од -1 до +1 кога x зема вредности од \(-3\pi \) до \(3\pi \) . И синусните и косинусните вредности на тригонометриската функција се повторуваат по интервал од \(2\pi \) .
Синус е прикажан како солидна линија, а косинус како испрекината линија.
Дозволете ни да решиме неколку примери врз основа на горенаведените тригонометриски функции:
Пример 1: Ако \(\cos x\) = − 4/5, x лежи во третиот квадрант, најдете ги вредностите на другите пет тригонометриски функции.
Решение: Видете ги табелите дадени погоре.
Како \(\cos x\) = -4/5, затоа \(\sec x\) = -5/4
Како \(\mathbf{ \cos^2 x + \sin^2x = 1}\) така \({16\over25} + \sin^2x = 1 ⇒ \sin^2x = 1-\frac{16}{25} = {9\over25}\)
\(\sin x = \pm3/5\)
Бидејќи x лежи во вредноста на третиот квадрант, така \(\sin x\) ќе биде негативно (видете ја табелата со знаци за квадрант). Затоа \(\sin x\) = -3/5 и \(\csc x \) = -5/3
Како \(\tan x = \sin x/\cos x\) , затоа \(\tan x\) = \(\frac{-4/5}{-3/5}\) = 4/3 Пример
2 : Најдете ја вредноста на \(\cos(5\pi/2)\)
Решение: \(\cos(5\pi/2) = \cos (2\pi + {1\pi}/_2)\)
Бидејќи вредноста на косинус се повторува по \(2\pi \) затоа \(\cos(2\pi + {1\pi}/_2) = \cos(\pi/2) = 0\)