Бид тэгш өнцөгт гурвалжны хурц өнцгийг талуудын харьцаагаар хэрхэн хэмжихийг мэддэг тул радиан хэмжүүрийн хувьд дурын өнцөгт тригонометрийн харьцааг сурч, тэдгээрийг тригонометрийн функц болгон судлах цаг болжээ.
Төв нь координатын тэнхлэгийн эхлэл дээр байрладаг нэгж радиустай тойргийг авч үзье.
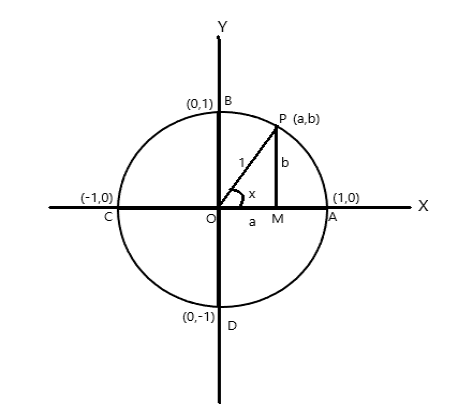
A = (1,0), B = (0,1), C = (-1,0) ба D = (0,-1) -ийн координатын цэгүүд
\(\angle AOP = x \) радиантай тойрог дээрх дурын цэг P (a,b) байг. Тиймээс нумын урт \(AP = x \) нэгж.
\(\cos x = a\) , \(\sin x = b\) . \(\bigtriangleup POM\) нь тэгш өнцөгт гурвалжин учир \(OP^2 = OM^2 + PM^2\)
тиймээс \(1 = a^2 + b^2\)
| \(\mathbf{ \cos^2 x + \sin^2x = 1}\) |
Нэг бүтэн эргэлт нь тойргийн төвд \(2\pi\) радианы өнцөгтэй байх тул. Дээрх зургаас
\(\angle AOB = \pi/2 \)
\(\angle AOC = \pi\)
\(\angle AOD = \frac{3\pi}{2} \)
Бид \(\cos x = \frac {\textrm {Base}}{\textrm{Hypotenuse}}\) ба \(\sin x = \frac {\textrm {Perpendicular}}{\textrm{Hypotenuse}}\)
\(\cos0^\circ = 1\) \(\sin0^\circ = 0\)
\(\cos\frac{\pi}{2} = 0\) \(\sin\frac{\pi}{2} = 1\)
\(\cos\pi = -1\) \(\sin\pi = 0\)
\(\cos2\pi = 1\) \(\sin2\pi = 0\)
P цэгээс нэг бүтэн эргэлт хийснээр бид дахин P цэгт хүрнэ \(\cos x\) ба \(\sin x\) ийн утга ижил хэвээр байгаа тул бид ингэж хэлж болно.
x нь \(2\pi\) -ийн интеграл үржвэрээр нэмэгдэх эсвэл буурахад синусын утга, косинусын функц өөрчлөгдөхгүй. Тиймээс,
\(\sin(n\cdot2\pi + x) = \sin x\)
\(\cos(n\cdot 2\pi + x) = \cos x \)
Энд n нь бүхэл тоо.
\(\space x = n\pi\) үед \(\sin x = 0\) байгааг бид анзаарах болно.
ба \(\cos x = 0\) үед \(x = (2n+1)\pi/2\)
Бусад тригонометрийн функцуудыг синус болон косинусын функцээр гаргах.
| \(\mathbf{\csc x} = \mathbf{\frac{1}{\sin x}}\) энд \(x \neq n\pi\) |
| \(\mathbf{\sec x } = \mathbf{\frac{1}{\cos x}}\) энд |
| \(\mathbf{\tan x } = \mathbf{\frac{\sin x}{\cos x}}\) энд |
| \(\mathbf{\cot x } = \mathbf{\frac{\cos x}{\sin x}}\) энд \( x \neq n\pi\) |
| \(\textbf 1 + \mathbf {\tan^2x = \sec^2x}\) |
| \(\textbf 1 + \mathbf {\cot^2x = \csc^2x}\) |
Доорх хүснэгтэд тригонометрийн функцүүдийн тэмдэг, утга нь янз бүрийн квадратуудад хэрхэн өөрчлөгдөж байгааг харуулж байна.
| I | II | III | IV | дөрвөлжин |
| sinx | + | + | − | − |
| cosx | + | − | − | + |
| tanx | + | − | + | − |
| cosecx | + | + | − | − |
| secx | + | − | − | + |
| cotx | + | − | + | − |
0°, 30°, 45°, 60°, 90° зэрэг тригонометрийн өнцгийн утгыг харуулсан доорх хүснэгтийг харна уу.
Өнцөг(градус ба радианаар) | sin | cos | tan | cot | csc | сек |
| 0° | 0 | 1 | 0 | ∞ | ∞ | 1 |
| 30° эсвэл π/6 радиан | 1/2 | √3/2 | 1/√3 | √3 | 2 | 2/√3 |
| 45 ° эсвэл π/4 радиан | 1/√2 | 1/√2 | 1 | 1 | √2 | √2 |
| 60° буюу π/3 радиан | √3/2 | 1/2 | √3 | 1/ √3 | 2/√3 | 2 |
| 90° буюу π/2 радиан | 1 | 0 | ∞ | 0 | 1 | ∞ |
| 180° эсвэл π радиан | 0 | -1 | 0 | ∞ | ∞ | -1 |
| 270 | ° буюу 3π/2 радиан | -1 | 0 | ∞0 | - 1 | ∞ |
| 360° буюу 2π радиан | 0 | 1 | 0 | ∞ | ∞ | 1 |
Дээрх хүснэгтийг ажиглавал:
(\mathbf{\tan x = \cot(90^\circ)\(\mathbf{\sin x = \cos(90^\circ-x)}\) |
| \(\mathbf{\tan x = \cot(90^\circ-x)}\) |
| \(\mathbf{\tan x = \cot(90^\circ-x)}\) |
| \(\mathbf{\sec x = \csc(90^\circ-x) }\) |
| \(\mathbf{\csc x = \sec(90^\circ-x)}\) |
| \( \mathbf{ \sin(-x) = -\sin x}\) |
| \( \mathbf{ \cos(-x) = \cos x}\) |
| \(\tan(-x) = -\tan x\) |
\(\sin x\) ба \(\cos x\) -ийн график дүрслэл нь x нь \(-3\pi \) -ээс \(3\pi \) хүртэлх утгыг авах үед -1-ээс +1 хооронд хэлбэлздэг. . Тригонометрийн функцийн синус ба косинусын утгууд хоёулаа \(2\pi \) интервалын дараа давтана.
Синусыг хатуу шугамаар, косинусыг тасархай шугамаар харуулав.
Дээрх тригонометрийн функцууд дээр үндэслэн хэдэн жишээг шийдье.
Жишээ 1: Хэрэв \(\cos x\) = − 4/5 бол x нь 3-р квадратад байгаа бол бусад таван тригонометрийн функцийн утгыг ол.
Шийдэл: Дээрх хүснэгтүүдийг харна уу.
\(\cos x\) = -4/5 тул \(\sec x\) = -5/4
\(\mathbf{ \cos^2 x + \sin^2x = 1}\) болохоор \({16\over25} + \sin^2x = 1 ⇒ \sin^2x = 1-\frac{16}{25} = {9\over25}\)
\(\sin x = \pm3/5\)
Гурав дахь квадрат утгад х байх тул \(\sin x\) сөрөг байх болно(квадрантын тэмдгийн хүснэгтийг үзнэ үү). Тиймээс \(\sin x\) = -3/5 ба \(\csc x \) = -5/3
\(\tan x = \sin x/\cos x\) тул \(\tan x\) = \(\frac{-4/5}{-3/5}\) = 4/3
Жишээ 2 : \(\cos(5\pi/2)\) ийн утгыг ол
Шийдэл: \(\cos(5\pi/2) = \cos (2\pi + {1\pi}/_2)\)
Косинусын утга \(2\pi \) -ын дараа давтагдах тул \(\cos(2\pi + {1\pi}/_2) = \cos(\pi/2) = 0\)