Back to the topics list

trigonometric လုပ်ဆောင်ချက်များကို

၎င်း၏နှစ်ဖက်အချိုးအစားအဖြစ် ညာဘက်တြိဂံအတွက် စူးရှသောထောင့်ကို တိုင်းတာနည်းကို ကျွန်ုပ်တို့သိထားသောကြောင့်၊ ၎င်းသည် မည်သည့်ထောင့်မှ မည်သည့်ထောင့်သို့မဆို အရေဒီယံတိုင်းတာမှုနှင့် Trigonometric လုပ်ဆောင်ချက်များအဖြစ် လေ့လာရန် အချိန်တန်ပြီဖြစ်သည်။

အချင်းဝက်၏ အလယ်ဗဟိုသည် သြဒီနိတ်ပုဆိန်တွင်ရှိသော ယူနစ်အချင်းဝက် စက်ဝိုင်းတစ်ခုကို သုံးသပ်ကြည့်ပါ။

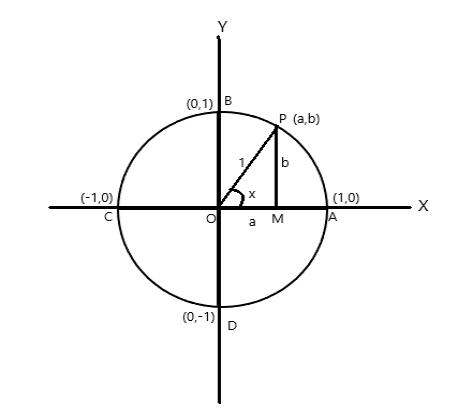
A=(1,0), B=(0,1), C=(-1,0) နှင့် D=(0,-1)၊
P (a,b) သည် စက်ဝိုင်းပေါ်ရှိ မည်သည့်အမှတ်ကိုမဆို \(\angle AOP = x \) radian ဖြစ်ပါစေ။ ထို့ကြောင့် arc \(AP = x \) ယူနစ်၏ အရှည်။
\(\cos x = a\) ၊ \(\sin x = b\) ။ \(\bigtriangleup POM\) သည် ညာထောင့်တြိဂံဖြစ်သောကြောင့် \(OP^2 = OM^2 + PM^2\)
ထို့ကြောင့် \(1 = a^2 + b^2\) ⇒

ပြီးပြည့်စုံသောတော်လှန်ရေးတစ်ခုသည် စက်ဝိုင်း၏အလယ်ဗဟိုတွင် \(2\pi\) radian ထောင့်ကို ရောက်သွားသောကြောင့်ဖြစ်သည်။ အထက်ပါပုံမှ
\(\angle AOB = \pi/2 \)
\(\angle AOC = \pi\)
\(\angle AOD = \frac{3\pi}{2} \)
\(\cos x = \frac {\textrm {Base}}{\textrm{Hypotenuse}}\) နှင့် \(\sin x = \frac {\textrm {Perpendicular}}{\textrm{Hypotenuse}}\)
\(\cos0^\circ = 1\) \(\sin0^\circ = 0\)
\(\cos\frac{\pi}{2} = 0\) \(\sin\frac{\pi}{2} = 1\)
\(\cos\pi = -1\) \(\sin\pi = 0\)
\(\cos2\pi = 1\) \(\sin2\pi = 0\)

အမှတ် P မှ ပြီးပြည့်စုံသော တော်လှန်ရေးတစ်ခုကို ခံယူလိုက်သည်နှင့်အမျှ အမှတ် P သို့ ရောက်ရှိသွားပြန်သည် \(\cos x\) နှင့် \(\sin x\) တို့၏တန်ဖိုးသည် အတူတူပင်ဖြစ်တော့သည်ဟု ဆိုနိုင်ပါသည်။
x သည် \(2\pi\) ၏ ပေါင်းစပ်ကိန်းဂဏန်းတစ်ခုဖြင့် တိုးခြင်း သို့မဟုတ် လျော့ခြင်းကြောင့်၊ sine ၏တန်ဖိုး၊ cosine လုပ်ဆောင်ချက်သည် ပြောင်းလဲခြင်းမရှိပါ။ ထို့ကြောင့်,

\(\sin(n\cdot2\pi + x) = \sin x\)

\(\cos(n\cdot 2\pi + x) = \cos x \)
n က ကိန်းပြည့်ဘယ်မှာလဲ။
\(\sin x = 0\) က \(\space x = n\pi\) ဆိုတာကို သတိထားမိမှာပါ၊
နှင့် \(\cos x = 0\) အခါ \(x = (2n+1)\pi/2\)

sine နှင့် cosine လုပ်ဆောင်ချက်များအရ အခြားသော trigonometric functions များကို ရယူခြင်း။

\(\cos^2 x + \sin^2x = 1\) အသုံးပြု၍ အောက်ပါ ဖော်မြူလာများကို ရယူနိုင်ပါသည်။

Trigonometric Functions ၏ သင်္ကေတ

အောက်ဖော်ပြပါဇယားသည် မတူညီသော quadrants များတွင် trigonometric လုပ်ဆောင်ချက်များ၏ နိမိတ်လက္ခဏာနှင့် တန်ဖိုးများ ပြောင်းလဲပုံကို ပြသထားသည်။

0°၊ 30°၊ 45°၊ 60° နှင့် 90° ကဲ့သို့သော ဒီဂရီများအတွက် trigonometric ထောင့်များ၏တန်ဖိုးကိုပြသသည့်အောက်ပါဇယားကိုကြည့်ပါ။

အထက်ဖော်ပြပါဇယားကို လေ့လာကြည့်လျှင် သင်သတိပြုမိလိမ့်မည်-

x မှ တန်ဖိုးများ \(-3\pi \) မှ \(3\pi \) သို့ ယူသောအခါ y သည် -1 မှ +1 အထိ ကွာဝေးသည့် \ \(\sin x\) နှင့် \(\cos x\) တို့၏ ဂရပ်ဖစ် ကိုယ်စားပြုမှု ဖြစ်သည်။ trigonometric function နှစ်ခုလုံးသည် sine နှင့် cosine တန်ဖိုးများ \(2\pi \) ၏ကြားကာလတစ်ခုပြီးနောက် ထပ်လုပ်ပါသည်။

Sine ကို အစိုင်အခဲမျဉ်းအဖြစ် ပြသထားပြီး Cosine ကို အစက်ချမျဉ်းအဖြစ် ပြထားသည်။

အထက်ဖော်ပြပါ trigonometric လုပ်ဆောင်ချက်များကို အခြေခံ၍ ဥပမာအချို့ကို ဖြေရှင်းကြပါစို့။

ဥပမာ 1- \(\cos x\) = − 4/5၊ x သည် တတိယ quadrant တွင် ရှိပါက၊ အခြား trigonometric function ငါးခု၏ တန်ဖိုးများကို ရှာပါ။

ဖြေရှင်းချက်- အထက်ဖော်ပြပါဇယားများကို ကိုးကားပါ။
\(\cos x\) = -4/5၊ ထို့ကြောင့် \(\sec x\) = -5/4
\(\mathbf{ \cos^2 x + \sin^2x = 1}\) ထို့ကြောင့် \({16\over25} + \sin^2x = 1 ⇒ \sin^2x = 1-\frac{16}{25} = {9\over25}\)
\(\sin x = \pm3/5\)
x သည် တတိယမြောက် quadrant တန်ဖိုးတွင် တည်ရှိသောကြောင့် \(\sin x\) သည် အနုတ် (quadrant sign table ကို ကိုးကားပါ)။ ထို့ကြောင့် \(\sin x\) = -3/5 နှင့် \(\csc x \) = -5/3
\(\tan x = \sin x/\cos x\) ထို့ကြောင့် \(\tan x\) = \(\frac{-4/5}{-3/5}\) = 4/3

ဥပမာ 2- \(\cos(5\pi/2)\) ၏တန်ဖိုးကို ရှာပါ
ဖြေရှင်းချက်-   \(\cos(5\pi/2) = \cos (2\pi + {1\pi}/_2)\)
ကိုsine ၏တန်ဖိုးသည် \(2\pi \) ပြီးနောက် ထပ်ခါတလဲလဲဖြစ်သောကြောင့် \(\cos(2\pi + {1\pi}/_2) = \cos(\pi/2) = 0\)