हामी जान्दछौं कि दायाँ त्रिभुजको लागि तीव्र कोणलाई यसको पक्षहरूको अनुपातको रूपमा कसरी मापन गर्ने, यो समय हो कि त्रिभुज मापनको सन्दर्भमा कुनै पनि कोणमा त्रिकोणमितीय अनुपातहरू सिक्ने र तिनीहरूलाई त्रिकोणमितीय प्रकार्यहरूको रूपमा अध्ययन गर्ने समय हो।
एकाइ त्रिज्याको सर्कललाई विचार गर्नुहोस्, जसको केन्द्र समन्वय अक्षको उत्पत्तिमा छ।
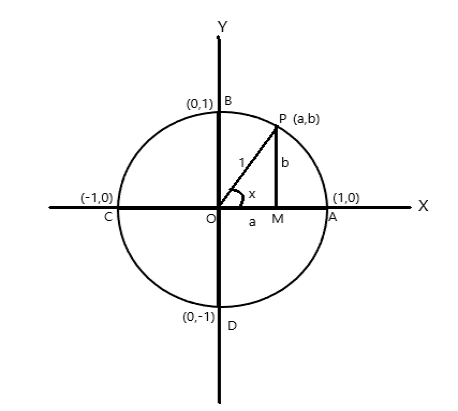
A = (1,0), B = (0,1), C = (-1,0) र D = (0,-1) को समन्वय बिन्दुहरू
P (a,b) लाई \(\angle AOP = x \) radian भएको वृत्तको कुनै पनि बिन्दु होस्। त्यसैले चाप \(AP = x \) एकाइको लम्बाइ।
\(\cos x = a\) , \(\sin x = b\) । जसरी \(\bigtriangleup POM\) एक समकोण त्रिकोण हो, \(OP^2 = OM^2 + PM^2\)
त्यसैले \(1 = a^2 + b^2\)
| \(\mathbf{ \cos^2 x + \sin^2x = 1}\) |
एउटा पूर्ण क्रान्तिले वृत्तको केन्द्रमा \(2\pi\) रेडियनको कोण घटाउँछ। माथिको चित्रबाट
\(\angle AOB = \pi/2 \)
\(\angle AOC = \pi\)
\(\angle AOD = \frac{3\pi}{2} \)
हामीलाई थाहा छ \(\cos x = \frac {\textrm {Base}}{\textrm{Hypotenuse}}\) र \(\sin x = \frac {\textrm {Perpendicular}}{\textrm{Hypotenuse}}\)
\(\cos0^\circ = 1\) \(\sin0^\circ = 0\)
\(\cos\frac{\pi}{2} = 0\) \(\sin\frac{\pi}{2} = 1\)
\(\cos\pi = -1\) \(\sin\pi = 0\)
\(\cos2\pi = 1\) \(\sin2\pi = 0\)
बिन्दु P बाट एक पूर्ण क्रान्ति गर्दा हामी फेरि P बिन्दुमा पुग्छौं \(\cos x\) र \(\sin x\) को मान उस्तै रहन्छ, त्यसैले हामी भन्न सक्छौं।
x लाई \(2\pi\) को अभिन्न गुणनले बढाउँछ वा घटाउँछ, sine को मान, कोसाइन प्रकार्य परिवर्तन हुँदैन। यसरी,
\(\sin(n\cdot2\pi + x) = \sin x\)
\(\cos(n\cdot 2\pi + x) = \cos x \)
जहाँ n पूर्णांक हो।
हामी याद गर्नेछौं कि \(\sin x = 0\) जब \(\space x = n\pi\)
र \(\cos x = 0\) जब \(x = (2n+1)\pi/2\)
साइन र कोसाइन प्रकार्यहरूको सन्दर्भमा अन्य त्रिकोणमितीय प्रकार्यहरू प्राप्त गर्दै।
| \(\mathbf{\csc x} = \mathbf{\frac{1}{\sin x}}\) जहाँ \(x \neq n\pi\) |
| \(\mathbf{\sec x } = \mathbf{\frac{1}{\cos x}}\) जहाँ |
| \(\mathbf{\tan x } = \mathbf{\frac{\sin x}{\cos x}}\) जहाँ |
| \(\mathbf{\cot x } = \mathbf{\frac{\cos x}{\sin x}}\) जहाँ \( x \neq n\pi\) |
| \(\textbf 1 + \mathbf {\tan^2x = \sec^2x}\) |
| \(\textbf 1 + \mathbf {\cot^2x = \csc^2x}\) |
तलको तालिकाले कसरी त्रिकोणमितीय कार्यहरूको चिन्ह र मान विभिन्न चतुर्भुजहरूमा परिवर्तन हुन्छ देखाउँछ।
| चतुर्थांश | म | II | III | IV |
| sinx | + | + | - | - |
| cosx | + | - | - | + |
| ट्यान्क्स | + | - | + | - |
| cosecx | + | + | - | - |
| secx | + | - | - | + |
| cotx | + | - | + | - |
0°, 30°, 45°, 60°, र 90° जस्ता डिग्रीहरूको लागि त्रिकोणमितीय कोणहरूको मान देखाउने तलको तालिकामा हेर्नुहोस्।
कोण (डिग्री र रेडियन मा) | पाप | cos | ट्यान | खाट | csc | सेकेन्ड |
| ०° | ० | १ | ० | ∞ | ∞ | १ |
| 30° वा π/6 रेडियन | १/२ | √3/2 | १/√३ | √३ | २ | २/√३ |
| ४५° वा π/४ रेडियन | १/√२ | १/√२ | १ | १ | √2 | √२ |
| ६०° वा π/३ रेडियन | √3/2 | १/२ | √३ | १/√३ | २/√३ | २ |
| ९०° वा π/२ रेडियन | १ | ० | ∞ | ० | १ | ∞ |
| 180° वा π रेडियन | ० | -१ | ० | ∞ | ∞ | -१ |
| 270° वा 3π/2 रेडियन | -१ | ० | ∞ | ० | -१ | ∞ |
| 360° वा 2π रेडियन | ० | १ | ० | ∞ | ∞ | १ |
माथिको तालिका अवलोकन गर्नुहोस्, तपाईंले याद गर्नुहुनेछ कि:
\(\mathbf{\sin x = \cos(90^\circ-x)}\) |
| \(\mathbf{\tan x = \cot(90^\circ-x)}\) |
| \(\mathbf{\sec x = \csc(90^\circ-x) }\) |
| \(\mathbf{\csc x = \sec(90^\circ-x)}\) |
| \( \mathbf{ \sin(-x) = -\sin x}\) |
| \( \mathbf{ \cos(-x) = \cos x}\) |
| \(\tan(-x) = -\tan x\) |
\(\sin x\) र \(\cos x\) को ग्राफिकल प्रतिनिधित्व जहाँ y -1 देखि +1 सम्म हुन्छ जब x \(-3\pi \) बाट \(3\pi \) मान लिन्छ। दुबै त्रिकोणमितीय प्रकार्य साइन र कोसाइन मानहरू \(2\pi \) को अन्तराल पछि दोहोर्याउँछन्।
साइनलाई ठोस रेखा र कोसाइनलाई डटेड रेखाको रूपमा देखाइएको छ।
माथिको त्रिकोणमितीय प्रकार्यहरूमा आधारित केही उदाहरणहरू समाधान गरौं:
उदाहरण १: यदि \(\cos x\) = − 4/5, x तेस्रो चतुर्भुजमा छ भने, अन्य पाँच त्रिकोणमितीय कार्यहरूको मान पत्ता लगाउनुहोस्।
समाधान: माथि दिइएको तालिकालाई सन्दर्भ गर्नुहोस्।
जस्तै \(\cos x\) = -4/5, त्यसैले \(\sec x\) = -5/4
जस्तै \(\mathbf{ \cos^2 x + \sin^2x = 1}\) त्यसैले \({16\over25} + \sin^2x = 1 ⇒ \sin^2x = 1-\frac{16}{25} = {9\over25}\)
\(\sin x = \pm3/5\)
x तेस्रो चतुर्भुज मानमा रहेको हुनाले \(\sin x\) ऋणात्मक हुनेछ (चतुर्भुज चिन्ह तालिकालाई हेर्नुहोस्)। त्यसैले \(\sin x\) = -3/5 र \(\csc x \) = -5/3
जस्तै \(\tan x = \sin x/\cos x\) , त्यसैले \(\tan x\) = \(\frac{-4/5}{-3/5}\) = 4/3
उदाहरण २: \(\cos(5\pi/2)\) को मान पत्ता लगाउनुहोस्
समाधान: \(\cos(5\pi/2) = \cos (2\pi + {1\pi}/_2)\)
कोसाइनको मान \(2\pi \) पछि दोहोरिन्छ त्यसैले, \(\cos(2\pi + {1\pi}/_2) = \cos(\pi/2) = 0\)