Aangezien we weten hoe we een scherpe hoek voor de rechthoekige driehoek moeten meten als de verhouding van de zijden, is het tijd om trigonometrische verhoudingen tot elke hoek te leren in termen van radiale maat en deze te bestuderen als trigonometrische functies.
Beschouw een cirkel met een eenheidsradius, waarvan het middelpunt bij de oorsprong van de coördinatenassen ligt.
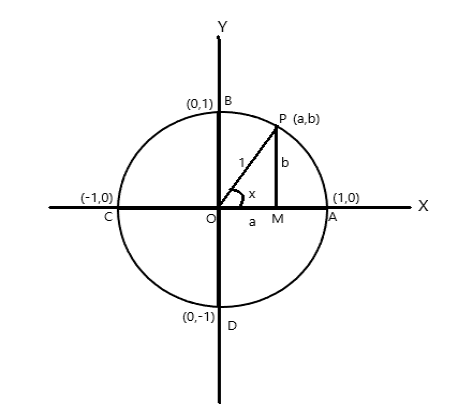
Coördinaatpunten van A = (1,0), B = (0,1), C = (-1,0) en D = (0,-1)
Zij P (a,b) een willekeurig punt op de cirkel met \(\angle AOP = x \) radiaal. Daarom is de lengte van boog \(AP = x \) eenheid.
\(\cos x = a\) , \(\sin x = b\) . Omdat \(\bigtriangleup POM\) een rechthoekige driehoek is, \(OP^2 = OM^2 + PM^2\)
daarom \(1 = a^2 + b^2\)
| \(\mathbf{ \cos^2 x + \sin^2x = 1}\) |
Omdat één volledige omwenteling in het middelpunt van de cirkel een hoek van \(2\pi\) radiaal insluit. Uit bovenstaande figuur
\(\angle AOB = \pi/2 \)
\(\angle AOC = \pi\)
\(\angle AOD = \frac{3\pi}{2} \)
We weten \(\cos x = \frac {\textrm {Base}}{\textrm{Hypotenuse}}\) en \(\sin x = \frac {\textrm {Perpendicular}}{\textrm{Hypotenuse}}\)
\(\cos0^\circ = 1\) \(\sin0^\circ = 0\)
\(\cos\frac{\pi}{2} = 0\) \(\sin\frac{\pi}{2} = 1\)
\(\cos\pi = -1\) \(\sin\pi = 0\)
\(\cos2\pi = 1\) \(\sin2\pi = 0\)
Als we vanuit punt P een volledige omwenteling nemen, bereiken we weer punt P. De waarde van \(\cos x\) en \(\sin x\) blijft hetzelfde, dus kunnen we zeggen dat
als x toeneemt of afneemt met een geheel veelvoud van \(2\pi\) , verandert de waarde van sinus, cosinusfunctie niet. Dus,
\(\sin(n\cdot2\pi + x) = \sin x\)
\(\cos(n\cdot 2\pi + x) = \cos x \)
waarbij n een geheel getal is.
We zullen merken dat \(\sin x = 0\) wanneer \(\space x = n\pi\)
en \(\cos x = 0\) als \(x = (2n+1)\pi/2\)
Andere trigonometrische functies afleiden in termen van sinus- en cosinusfuncties.
| \(\mathbf{\csc x} = \mathbf{\frac{1}{\sin x}}\) waarin \(x \neq n\pi\) |
| \(\mathbf{\sec x } = \mathbf{\frac{1}{\cos x}}\) waarbij |
| \(\mathbf{\tan x } = \mathbf{\frac{\sin x}{\cos x}}\) waarbij |
| \(\mathbf{\cot x } = \mathbf{\frac{\cos x}{\sin x}}\) waarin \( x \neq n\pi\) |
| \(\textbf 1 + \mathbf {\tan^2x = \sec^2x}\) |
| \(\textbf 1 + \mathbf {\cot^2x = \csc^2x}\) |
Onderstaande tabel laat zien hoe het teken en de waarde van trigonometrische functies veranderen in verschillende kwadranten.
| kwadranten | I | II | III | IV |
| sinx | + | + | − | − |
| cosx | + | − | − | + |
| tanx | + | − | + | − |
| cosecx | + | + | − | − |
| sec | + | − | − | + |
| cotx | + | − | + | − |
Bekijk de onderstaande tabel met de waarde van trigonometrische hoeken voor graden zoals 0°, 30°, 45°, 60° en 90°.
Hoeken (in graden & radialen) | zonde | cos | bruinen | kinderbed | csc | sec |
| 0° | 0 | 1 | 0 | ∞ | ∞ | 1 |
| 30° of π/6 radiaal | 1/2 | √3/2 | 1/√3 | √3 | 2 | 2/√3 |
| 45° of π/4 radiaal | 1/√2 | 1/√2 | 1 | 1 | √2 | √2 |
| 60° of π/3 radiaal | √3/2 | 1/2 | √3 | 1/√3 | 2/√3 | 2 |
| 90° of π/2 radiaal | 1 | 0 | ∞ | 0 | 1 | ∞ |
| 180° of π radiaal | 0 | -1 | 0 | ∞ | ∞ | -1 |
| 270° of 3π/2 radiaal | -1 | 0 | ∞ | 0 | -1 | ∞ |
| 360° of 2π radiaal | 0 | 1 | 0 | ∞ | ∞ | 1 |
Let op de bovenstaande tabel, u zult merken dat:
\(\mathbf{\sin x = \cos(90^\circ-x)}\) |
| \(\mathbf{\tan x = \cot(90^\circ-x)}\) |
| \(\mathbf{\sec x = \csc(90^\circ-x) }\) |
| \(\mathbf{\csc x = \sec(90^\circ-x)}\) |
| \( \mathbf{ \sin(-x) = -\sin x}\) |
| \( \mathbf{ \cos(-x) = \cos x}\) |
| \(\tan(-x) = -\tan x\) |
Grafische weergave van \(\sin x\) en \(\cos x\) waarbij y varieert van -1 tot +1 wanneer x waarden aanneemt van \(-3\pi \) tot \(3\pi \) . Zowel de sinus- als de cosinuswaarden van de trigonometrische functie worden herhaald na een interval van \(2\pi \) .
Sinus wordt weergegeven als een ononderbroken lijn en cosinus als een stippellijn.
Laten we een paar voorbeelden oplossen op basis van de bovenstaande trigonometrische functies:
Voorbeeld 1: Als \(\cos x\) = − 4/5, x in het derde kwadrant ligt, zoek dan de waarden van de andere vijf goniometrische functies.
Oplossing: Raadpleeg de bovenstaande tabellen.
Als \(\cos x\) = -4/5, dus \(\sec x\) = -5/4
Als \(\mathbf{ \cos^2 x + \sin^2x = 1}\) dus \({16\over25} + \sin^2x = 1 ⇒ \sin^2x = 1-\frac{16}{25} = {9\over25}\)
\(\sin x = \pm3/5\)
Aangezien x in het derde kwadrant ligt, zal \(\sin x\) negatief zijn (zie de kwadranttekentabel). Dus \(\sin x\) = -3/5 en \(\csc x \) = -5/3
Als \(\tan x = \sin x/\cos x\) , dus \(\tan x\) = \(\frac{-4/5}{-3/5}\) = 4/3
Voorbeeld 2: Vind de waarde van \(\cos(5\pi/2)\)
Oplossing: \(\cos(5\pi/2) = \cos (2\pi + {1\pi}/_2)\)
Aangezien de waarde van cosinus zich herhaalt na \(2\pi \) \(\cos(2\pi + {1\pi}/_2) = \cos(\pi/2) = 0\)