Skoro już wiemy, jak zmierzyć kąt ostry trójkąta prostokątnego jako stosunek jego boków, nadszedł czas, aby nauczyć się stosunków trygonometrycznych do dowolnego kąta wyrażonych w radianach i przestudiować je jako funkcje trygonometryczne.
Rozważmy okrąg o jednostkowym promieniu, którego środek znajduje się na początku osi współrzędnych.
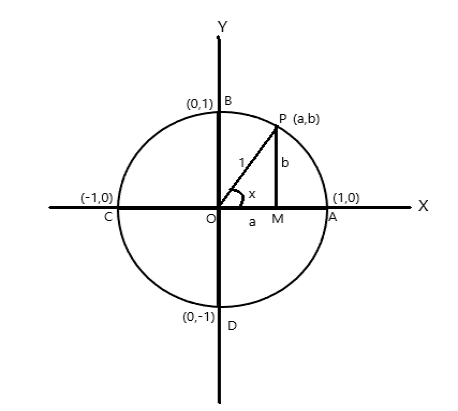
Współrzędne punktów A = (1,0), B = (0,1), C = (-1,0) i D = (0,-1)
Niech P (a,b) będzie dowolnym punktem na okręgu o \(\angle AOP = x \) radian. Dlatego długość łuku \(AP = x \) jednostka.
\(\cos x = a\) , \(\sin x = b\) . Ponieważ \(\bigtriangleup POM\) jest trójkątem prostokątnym, \(OP^2 = OM^2 + PM^2\)
zatem \(1 = a^2 + b^2\)
| \(\mathbf{ \cos^2 x + \sin^2x = 1}\) |
Ponieważ jeden pełny obrót obejmuje w środku koła kąt \(2\pi\) radianów. Z powyższego rysunku
\(\angle AOB = \pi/2 \)
\(\angle AOC = \pi\)
\(\angle AOD = \frac{3\pi}{2} \)
Wiemy \(\cos x = \frac {\textrm {Base}}{\textrm{Hypotenuse}}\) i \(\sin x = \frac {\textrm {Perpendicular}}{\textrm{Hypotenuse}}\)
\(\cos0^\circ = 1\) \(\sin0^\circ = 0\)
\(\cos\frac{\pi}{2} = 0\) \(\sin\frac{\pi}{2} = 1\)
\(\cos\pi = -1\) \(\sin\pi = 0\)
\(\cos2\pi = 1\) \(\sin2\pi = 0\)
Wykonując jeden pełny obrót od punktu P ponownie docieramy do punktu P. Wartość \(\cos x\) i \(\sin x\) pozostaje taka sama, stąd możemy powiedzieć, że
gdy x zwiększa się lub zmniejsza o całkowitą wielokrotność \(2\pi\) , wartość funkcji sinus, cosinus nie zmienia się. Zatem,
\(\sin(n\cdot2\pi + x) = \sin x\)
\(\cos(n\cdot 2\pi + x) = \cos x \)
gdzie n jest liczbą całkowitą.
Zauważmy, że \(\sin x = 0\) gdy \(\space x = n\pi\)
i \(\cos x = 0\) gdy \(x = (2n+1)\pi/2\)
Wyprowadzanie innych funkcji trygonometrycznych z funkcji sinus i cosinus.
| \(\mathbf{\csc x} = \mathbf{\frac{1}{\sin x}}\) gdzie \(x \neq n\pi\) |
| \(\mathbf{\sec x } = \mathbf{\frac{1}{\cos x}}\) gdzie |
| \(\mathbf{\tan x } = \mathbf{\frac{\sin x}{\cos x}}\) gdzie |
| \(\mathbf{\cot x } = \mathbf{\frac{\cos x}{\sin x}}\) gdzie \( x \neq n\pi\) |
| \(\textbf 1 + \mathbf {\tan^2x = \sec^2x}\) |
| \(\textbf 1 + \mathbf {\cot^2x = \csc^2x}\) |
Poniższa tabela pokazuje, jak zmieniają się znaki i wartości funkcji trygonometrycznych w różnych ćwiartkach.
| Kwadranty | I | II | III | IV |
| sinx | + | + | − | − |
| cosx | + | − | − | + |
| tanx | + | − | + | − |
| cosecx | + | + | − | − |
| secx | + | − | − | + |
| Cotx | + | − | + | − |
Spójrz na poniższą tabelę, która pokazuje wartości kątów trygonometrycznych dla stopni, takich jak 0°, 30°, 45°, 60° i 90°.
Kąty (w stopniach i radianach) | grzech | sałata | dębnik | łóżko składane | csc | sek |
| 0° | 0 | 1 | 0 | ∞ | ∞ | 1 |
| 30° lub π/6 radianów | 1/2 | √3/2 | 1/√3 | √3 | 2 | 2/√3 |
| 45° lub π/4 radiana | 1/√2 | 1/√2 | 1 | 1 | √2 | √2 |
| 60° lub π/3 radiana | 3/2 | 1/2 | √3 | 1/√3 | 2/√3 | 2 |
| 90° lub π/2 radiana | 1 | 0 | ∞ | 0 | 1 | ∞ |
| 180° lub π radian | 0 | -1 | 0 | ∞ | ∞ | -1 |
| 270° lub 3π/2 radiana | -1 | 0 | ∞ | 0 | -1 | ∞ |
| 360° lub 2π radianów | 0 | 1 | 0 | ∞ | ∞ | 1 |
Obserwuj powyższą tabelę, zauważysz, że:
\(\mathbf{\sin x = \cos(90^\circ-x)}\) |
| \(\mathbf{\tan x = \cot(90^\circ-x)}\) |
| \(\mathbf{\sec x = \csc(90^\circ-x) }\) |
| \(\mathbf{\csc x = \sec(90^\circ-x)}\) |
| \( \mathbf{ \sin(-x) = -\sin x}\) |
| \( \mathbf{ \cos(-x) = \cos x}\) |
| \(\tan(-x) = -\tan x\) |
Graficzna reprezentacja \(\sin x\) i \(\cos x\) gdzie y waha się od -1 do +1, gdy x przyjmuje wartości od \(-3\pi \) do \(3\pi \) . Zarówno sinus, jak i cosinus funkcji trygonometrycznych powtarzają się po przedziale \(2\pi \) .
Sinus jest pokazany jako linia ciągła, a cosinus jako linia kropkowana.
Rozwiążmy kilka przykładów w oparciu o powyższe funkcje trygonometryczne:
Przykład 1: Jeśli \(\cos x\) = − 4/5, x leży w trzeciej ćwiartce, znajdź wartości pozostałych pięciu funkcji trygonometrycznych.
Rozwiązanie: Zapoznaj się z tabelami podanymi powyżej.
Ponieważ \(\cos x\) = -4/5, więc \(\sec x\) = -5/4
Ponieważ \(\mathbf{ \cos^2 x + \sin^2x = 1}\) więc \({16\over25} + \sin^2x = 1 ⇒ \sin^2x = 1-\frac{16}{25} = {9\over25}\)
\(\sin x = \pm3/5\)
Ponieważ x leży w trzeciej ćwiartce, więc \(\sin x\) będzie ujemne (patrz tabela ze znakami ćwiartki). Dlatego \(\sin x\) = -3/5 i \(\csc x \) = -5/3
Ponieważ \(\tan x = \sin x/\cos x\) , więc \(\tan x\) = \(\frac{-4/5}{-3/5}\) = 4/3
Przykład 2: Znajdź wartość \(\cos(5\pi/2)\)
Rozwiązanie: \(\cos(5\pi/2) = \cos (2\pi + {1\pi}/_2)\)
Ponieważ wartość cosinusa powtarza się po \(2\pi \) , zatem \(\cos(2\pi + {1\pi}/_2) = \cos(\pi/2) = 0\)