Como sabemos como medir um ângulo agudo para o triângulo retângulo como a razão entre seus lados, é hora de aprender as razões trigonométricas para qualquer ângulo em termos de medida em radianos e estudá-las como funções trigonométricas.
Considere um círculo de raio unitário, cujo centro está na origem dos eixos de coordenadas.
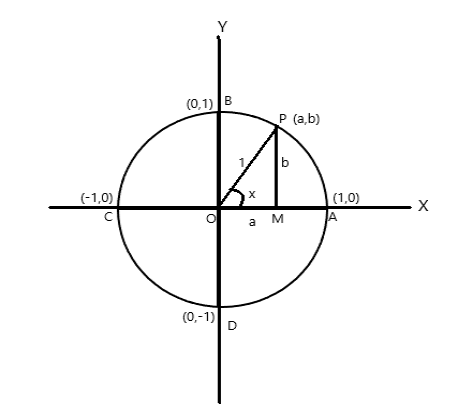
Pontos de coordenadas de A = (1,0), B = (0,1), C = (-1,0) e D = (0,-1)
Seja P (a,b) qualquer ponto da circunferência com \(\angle AOP = x \) radianos. Portanto o comprimento do arco \(AP = x \) unidade.
\(\cos x = a\) , \(\sin x = b\) . Como \(\bigtriangleup POM\) é um triângulo retângulo, \(OP^2 = OM^2 + PM^2\)
portanto \(1 = a^2 + b^2\)
| \(\mathbf{ \cos^2 x + \sin^2x = 1}\) |
Uma vez que uma revolução completa subtende no centro do círculo um ângulo de \(2\pi\) radianos. Da figura acima
\(\angle AOB = \pi/2 \)
\(\angle AOC = \pi\)
\(\angle AOD = \frac{3\pi}{2} \)
Sabemos \(\cos x = \frac {\textrm {Base}}{\textrm{Hypotenuse}}\) e \(\sin x = \frac {\textrm {Perpendicular}}{\textrm{Hypotenuse}}\)
\(\cos0^\circ = 1\) \(\sin0^\circ = 0\)
\(\cos\frac{\pi}{2} = 0\) \(\sin\frac{\pi}{2} = 1\)
\(\cos\pi = -1\) \(\sin\pi = 0\)
\(\cos2\pi = 1\) \(\sin2\pi = 0\)
Ao darmos uma volta completa a partir do ponto P, novamente alcançamos o ponto P. O valor de \(\cos x\) e \(\sin x\) permanece o mesmo, portanto podemos dizer que
conforme x aumenta ou diminui por um múltiplo inteiro de \(2\pi\) , o valor da função seno, cosseno não muda. Por isso,
\(\sin(n\cdot2\pi + x) = \sin x\)
\(\cos(n\cdot 2\pi + x) = \cos x \)
onde n é um número inteiro.
Notaremos que \(\sin x = 0\) quando \(\space x = n\pi\)
e \(\cos x = 0\) quando \(x = (2n+1)\pi/2\)
Derivação de outras funções trigonométricas em termos de funções seno e cosseno.
| \(\mathbf{\csc x} = \mathbf{\frac{1}{\sin x}}\) onde \(x \neq n\pi\) |
| \(\mathbf{\sec x } = \mathbf{\frac{1}{\cos x}}\) onde |
| \(\mathbf{\tan x } = \mathbf{\frac{\sin x}{\cos x}}\) onde |
| \(\mathbf{\cot x } = \mathbf{\frac{\cos x}{\sin x}}\) onde \( x \neq n\pi\) |
| \(\textbf 1 + \mathbf {\tan^2x = \sec^2x}\) |
| \(\textbf 1 + \mathbf {\cot^2x = \csc^2x}\) |
A tabela abaixo mostra como o sinal e o valor das funções trigonométricas mudam em diferentes quadrantes.
| quadrantes | EU | II | III | 4 |
| sinx | + | + | − | − |
| cosx | + | − | − | + |
| tanx | + | − | + | − |
| cosecx | + | + | − | − |
| secx | + | − | − | + |
| cox | + | − | + | − |
Dê uma olhada na tabela abaixo, que mostra o valor dos ângulos trigonométricos para graus como 0°, 30°, 45°, 60° e 90°.
Ângulos (em graus e radianos) | pecado | porque | bronzeado | berço | csc | segundo |
| 0° | 0 | 1 | 0 | ∞ | ∞ | 1 |
| 30° ou π/6 radianos | 1/2 | √3/2 | 1/√3 | √3 | 2 | 2/√3 |
| 45° ou π/4 radianos | 1/√2 | 1/√2 | 1 | 1 | √2 | √2 |
| 60° ou π/3 radianos | √3/2 | 1/2 | √3 | 1/√3 | 2/√3 | 2 |
| 90° ou π/2 radianos | 1 | 0 | ∞ | 0 | 1 | ∞ |
| 180° ou π radiano | 0 | -1 | 0 | ∞ | ∞ | -1 |
| 270° ou 3π/2 radianos | -1 | 0 | ∞ | 0 | -1 | ∞ |
| 360° ou 2π radianos | 0 | 1 | 0 | ∞ | ∞ | 1 |
Observe a tabela acima, você notará que:
\(\mathbf{\sin x = \cos(90^\circ-x)}\) |
| \(\mathbf{\tan x = \cot(90^\circ-x)}\) |
| \(\mathbf{\sec x = \csc(90^\circ-x) }\) |
| \(\mathbf{\csc x = \sec(90^\circ-x)}\) |
| \( \mathbf{ \sin(-x) = -\sin x}\) |
| \( \mathbf{ \cos(-x) = \cos x}\) |
| \(\tan(-x) = -\tan x\) |
Representação gráfica de \(\sin x\) e \(\cos x\) onde y varia de -1 a +1 quando x assume valores de \(-3\pi \) a \(3\pi \) . Ambos os valores de seno e cosseno da função trigonométrica se repetem após um intervalo de \(2\pi \) .
O seno é mostrado como uma linha sólida e o cosseno como uma linha pontilhada.
Vamos resolver alguns exemplos com base nas funções trigonométricas acima:
Exemplo 1: Se \(\cos x\) = − 4/5, x está no terceiro quadrante, encontre os valores das outras cinco funções trigonométricas.
Solução: Consulte as tabelas fornecidas acima.
Como \(\cos x\) = -4/5, portanto \(\sec x\) = -5/4
Como \(\mathbf{ \cos^2 x + \sin^2x = 1}\) então \({16\over25} + \sin^2x = 1 ⇒ \sin^2x = 1-\frac{16}{25} = {9\over25}\)
\(\sin x = \pm3/5\)
Como x está no valor do terceiro quadrante, então \(\sin x\) será negativo (consulte a tabela de sinais do quadrante). Portanto \(\sin x\) = -3/5 e \(\csc x \) = -5/3
Como \(\tan x = \sin x/\cos x\) , portanto \(\tan x\) = \(\frac{-4/5}{-3/5}\) = 4/3
Exemplo 2: Encontre o valor de \(\cos(5\pi/2)\)
Solução: \(\cos(5\pi/2) = \cos (2\pi + {1\pi}/_2)\)
Como o valor do cosseno se repete após \(2\pi \) , portanto, \(\cos(2\pi + {1\pi}/_2) = \cos(\pi/2) = 0\)