Поскольку мы знаем, как измерить острый угол прямоугольного треугольника как отношение его сторон, пришло время изучить тригонометрические отношения к любому углу в радианах и изучить их как тригонометрические функции.
Рассмотрим окружность единичного радиуса, центр которой находится в начале осей координат.
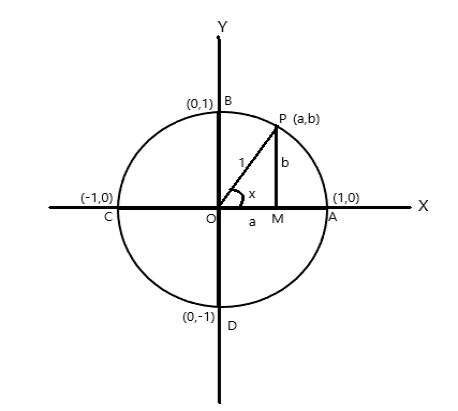
Координатные точки A = (1,0), B = (0,1), C = (-1,0) и D = (0,-1)
Пусть P (a,b) будет любой точкой на окружности с \(\angle AOP = x \) радиан. Поэтому длина дуги \(AP = x \) единица.
\(\cos x = a\) , \(\sin x = b\) . Поскольку \(\bigtriangleup POM\) является прямоугольным треугольником, \(OP^2 = OM^2 + PM^2\)
поэтому \(1 = a^2 + b^2\)
| \(\mathbf{ \cos^2 x + \sin^2x = 1}\) |
Поскольку один полный оборот образует в центре окружности угол \(2\pi\) радиан. Из приведенного выше рисунка
\(\angle AOB = \pi/2 \)
\(\angle AOC = \pi\)
\(\angle AOD = \frac{3\pi}{2} \)
Мы знаем \(\cos x = \frac {\textrm {Base}}{\textrm{Hypotenuse}}\) и \(\sin x = \frac {\textrm {Perpendicular}}{\textrm{Hypotenuse}}\)
\(\cos0^\circ = 1\) \(\sin0^\circ = 0\)
\(\cos\frac{\pi}{2} = 0\) \(\sin\frac{\pi}{2} = 1\)
\(\cos\pi = -1\) \(\sin\pi = 0\)
\(\cos2\pi = 1\) \(\sin2\pi = 0\)
Совершая один полный оборот из точки P, мы снова достигаем точки P. Значение \(\cos x\) и \(\sin x\) остается прежним, поэтому мы можем сказать, что
когда x увеличивается или уменьшается на целое число, кратное \(2\pi\) , значение функции синуса, косинуса не меняется. Таким образом,
\(\sin(n\cdot2\pi + x) = \sin x\)
\(\cos(n\cdot 2\pi + x) = \cos x \)
где n — целое число.
Заметим, что \(\sin x = 0\) когда \(\space x = n\pi\)
и \(\cos x = 0\) , когда \(x = (2n+1)\pi/2\)
Вывод других тригонометрических функций через функции синуса и косинуса.
| \(\mathbf{\csc x} = \mathbf{\frac{1}{\sin x}}\) где \(x \neq n\pi\) |
| \(\mathbf{\sec x } = \mathbf{\frac{1}{\cos x}}\) где |
| \(\mathbf{\tan x } = \mathbf{\frac{\sin x}{\cos x}}\) где |
| \(\mathbf{\cot x } = \mathbf{\frac{\cos x}{\sin x}}\) где \( x \neq n\pi\) |
| \(\textbf 1 + \mathbf {\tan^2x = \sec^2x}\) |
| \(\textbf 1 + \mathbf {\cot^2x = \csc^2x}\) |
В таблице ниже показано, как меняются знак и значение тригонометрических функций в разных квадрантах.
| Квадранты | я | II | III | IV |
| синкс | + | + | − | − |
| cosx | + | − | − | + |
| Танкс | + | − | + | − |
| cosecx | + | + | − | − |
| секкс | + | − | − | + |
| котекс | + | − | + | − |
Взгляните на приведенную ниже таблицу, в которой показано значение тригонометрических углов для таких градусов, как 0°, 30°, 45°, 60° и 90°.
Углы (в градусах и радианах) | грех | потому что | загар | детская кроватка | csc | сек |
| 0° | 0 | 1 | 0 | ∞ | ∞ | 1 |
| 30° или π/6 радиан | 1/2 | √3/2 | 1/√3 | √3 | 2 | 2/√3 |
| 45° или π/4 радиан | 1/√2 | 1/√2 | 1 | 1 | √2 | √2 |
| 60° или π/3 радиан | √3/2 | 1/2 | √3 | 1/√3 | 2/√3 | 2 |
| 90° или π/2 радиан | 1 | 0 | ∞ | 0 | 1 | ∞ |
| 180° или π радиан | 0 | -1 | 0 | ∞ | ∞ | -1 |
| 270° или 3π/2 радиан | -1 | 0 | ∞ | 0 | -1 | ∞ |
| 360° или 2π радиан | 0 | 1 | 0 | ∞ | ∞ | 1 |
Обратите внимание на приведенную выше таблицу, вы заметите, что:
\(\mathbf{\sin x = \cos(90^\circ-x)}\) |
| \(\mathbf{\tan x = \cot(90^\circ-x)}\) |
| \(\mathbf{\sec x = \csc(90^\circ-x) }\) |
| \(\mathbf{\csc x = \sec(90^\circ-x)}\) |
| \( \mathbf{ \sin(-x) = -\sin x}\) |
| \( \mathbf{ \cos(-x) = \cos x}\) |
| \(\tan(-x) = -\tan x\) |
Графическое представление \(\sin x\) и \(\cos x\) , где y находится в диапазоне от -1 до +1, когда x принимает значения от \(-3\pi \) до \(3\pi \) . Значения синуса и косинуса тригонометрической функции повторяются через интервал \(2\pi \) .
Синус показан сплошной линией, а косинус пунктирной линией.
Давайте решим несколько примеров на основе приведенных выше тригонометрических функций:
Пример 1. Если \(\cos x\) = − 4/5, x лежит в третьем квадранте, найдите значения остальных пяти тригонометрических функций.
Решение: Обратитесь к таблицам, приведенным выше.
Поскольку \(\cos x\) = -4/5, следовательно, \(\sec x\) = -5/4
Поскольку \(\mathbf{ \cos^2 x + \sin^2x = 1}\) то \({16\over25} + \sin^2x = 1 ⇒ \sin^2x = 1-\frac{16}{25} = {9\over25}\)
\(\sin x = \pm3/5\)
Поскольку x лежит в значении третьего квадранта, поэтому \(\sin x\) будет отрицательным (см. таблицу знаков квадранта). Поэтому \(\sin x\) = -3/5 и \(\csc x \) = -5/3
Поскольку \(\tan x = \sin x/\cos x\) , следовательно, \(\tan x\) = \(\frac{-4/5}{-3/5}\) = 4/3
Пример 2. Найдите значение \(\cos(5\pi/2)\)
Решение: \(\cos(5\pi/2) = \cos (2\pi + {1\pi}/_2)\)
Поскольку значение косинуса повторяется после \(2\pi \) \(\cos(2\pi + {1\pi}/_2) = \cos(\pi/2) = 0\)