Meqë dimë se si të matim një kënd të mprehtë për trekëndëshin kënddrejtë si raport i brinjëve të tij, është koha të mësojmë raportet trigonometrike ndaj çdo këndi për sa i përket masës së radianit dhe t'i studiojmë ato si funksione trigonometrike.
Konsideroni një rreth me rreze njësi, qendra e të cilit është në origjinën e boshtit koordinativ.
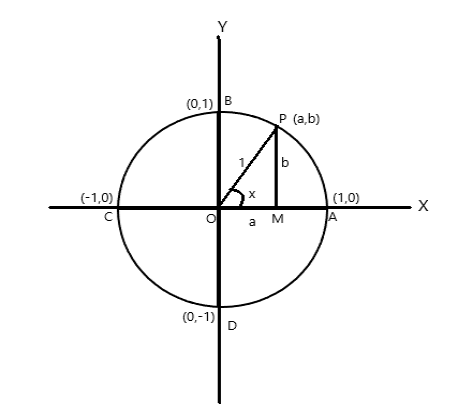
Pikat e koordinatave të A = (1,0), B = (0,1), C = (-1,0) dhe D = (0,-1)
Le të jetë P (a,b) çdo pikë në rreth me \(\angle AOP = x \) radian. Prandaj gjatësia e harkut \(AP = x \) njësi.
\(\cos x = a\) , \(\sin x = b\) . Pasi \(\bigtriangleup POM\) është një trekëndësh kënddrejtë, \(OP^2 = OM^2 + PM^2\)
prandaj \(1 = a^2 + b^2\)
| \(\mathbf{ \cos^2 x + \sin^2x = 1}\) |
Meqenëse një rrotullim i plotë nënshtrohet në qendër të rrethit një kënd prej \(2\pi\) radian. Nga figura e mësipërme
\(\angle AOB = \pi/2 \)
\(\angle AOC = \pi\)
\(\angle AOD = \frac{3\pi}{2} \)
Ne e dimë \(\cos x = \frac {\textrm {Base}}{\textrm{Hypotenuse}}\) dhe \(\sin x = \frac {\textrm {Perpendicular}}{\textrm{Hypotenuse}}\)
\(\cos0^\circ = 1\) \(\sin0^\circ = 0\)
\(\cos\frac{\pi}{2} = 0\) \(\sin\frac{\pi}{2} = 1\)
\(\cos\pi = -1\) \(\sin\pi = 0\)
\(\cos2\pi = 1\) \(\sin2\pi = 0\)
Ndërsa marrim një rrotullim të plotë nga pika P, përsëri arrijmë në pikën P. Vlera e \(\cos x\) dhe \(\sin x\) mbetet e njëjtë, prandaj mund të themi se
ndërsa x rritet ose zvogëlohet me një shumëfish integral të \(2\pi\) , vlera e funksionit sinus, kosinus nuk ndryshon. Kështu,
\(\sin(n\cdot2\pi + x) = \sin x\)
\(\cos(n\cdot 2\pi + x) = \cos x \)
ku n është një numër i plotë.
Do të vërejmë se \(\sin x = 0\) kur \(\space x = n\pi\)
dhe \(\cos x = 0\) kur \(x = (2n+1)\pi/2\)
Nxjerrja e funksioneve të tjera trigonometrike në funksion të sinusit dhe kosinusit.
| \(\mathbf{\csc x} = \mathbf{\frac{1}{\sin x}}\) ku \(x \neq n\pi\) |
| \(\mathbf{\sec x } = \mathbf{\frac{1}{\cos x}}\) ku |
| \(\mathbf{\tan x } = \mathbf{\frac{\sin x}{\cos x}}\) ku |
| \(\mathbf{\cot x } = \mathbf{\frac{\cos x}{\sin x}}\) ku \( x \neq n\pi\) |
| \(\textbf 1 + \mathbf {\tan^2x = \sec^2x}\) |
| \(\textbf 1 + \mathbf {\cot^2x = \csc^2x}\) |
Tabela e mëposhtme tregon se si shenja dhe vlera e funksioneve trigonometrike ndryshojnë në kuadrantë të ndryshëm.
| Kuadrantet | I | II | III | IV |
| sinx | + | + | − | − |
| cosx | + | − | − | + |
| tanx | + | − | + | − |
| cosecx | + | + | − | − |
| secx | + | − | − | + |
| cotx | + | − | + | − |
Shikoni tabelën e mëposhtme e cila tregon vlerën e këndeve trigonometrike për shkallë të tilla si 0°, 30°, 45°, 60° dhe 90°.
Këndet (në gradë dhe radian) | sin | cos | tan | cot | csc | sec |
| 0° | 0 | 1 | 0 | ∞ | ∞ | 1 |
| 30° ose π/6 radian | 1/2 | √3/2 | 1/√3 | √3 | 2 | 2/√3 |
| 45 ° ose π/4 radian | 1/√2 | 1/√2 | 1 | 1 | √2 | √2 |
| 60° ose π/3 radian | √3/2 | 1/2 | √3 | 1/ √3 | 2/√3 | 2 |
| 90° ose π/2 radian | 1 | 0 | ∞ | 0 | 1 | ∞ |
| 180° ose π radian | 0 | -1 | 0 | ∞ | ∞ | -1 |
| 270° ose 3π/2 radian | -1 | 0 | ∞ | 0 | - 1 | ∞ |
| 360° ose 2π radian | 0 | 1 | 0 | ∞ | ∞ | 1 |
Vëzhgoni tabelën e mësipërme, do të vini re se:
( \mathbf{\tan x = \cot(90^\circ\(\mathbf{\sin x = \cos(90^\circ-x)}\) |
| \(\mathbf{\tan x = \cot(90^\circ-x)}\) |
| \(\mathbf{\tan x = \cot(90^\circ-x)}\) |
| \(\mathbf{\sec x = \csc(90^\circ-x) }\) |
| \(\mathbf{\csc x = \sec(90^\circ-x)}\) |
| \( \mathbf{ \sin(-x) = -\sin x}\) |
| \( \mathbf{ \cos(-x) = \cos x}\) |
| \(\tan(-x) = -\tan x\) |
Paraqitja grafike e \(\sin x\) dhe \(\cos x\) ku y varion nga -1 në +1 kur x merr vlera nga \(-3\pi \) në \(3\pi \) . Të dy vlerat e sinusit dhe kosinusit të funksionit trigonometrik përsëriten pas një intervali prej \(2\pi \) .
Sinusi tregohet si vijë e fortë dhe kosinusi si vijë me pika.
Le të zgjidhim disa shembuj bazuar në funksionet trigonometrike të mësipërme:
Shembulli 1: Nëse \(\cos x\) = − 4/5, x shtrihet në kuadrantin e tretë, gjeni vlerat e pesë funksioneve të tjera trigonometrike.
Zgjidhja: Referojuni tabelave të dhëna më sipër.
Si \(\cos x\) = -4/5, prandaj \(\sec x\) = -5/4
Si \(\mathbf{ \cos^2 x + \sin^2x = 1}\) kështu \({16\over25} + \sin^2x = 1 ⇒ \sin^2x = 1-\frac{16}{25} = {9\over25}\)
\(\sin x = \pm3/5\)
Ndërsa x qëndron në vlerën e kuadrantit të tretë, kështu \(\sin x\) do të jetë negative (referojuni tabelës së shenjave të kuadrantit). Prandaj \(\sin x\) = -3/5 dhe \(\csc x \) = -5/3
Si \(\tan x = \sin x/\cos x\) , prandaj \(\tan x\) = \(\frac{-4/5}{-3/5}\) = 4/3 Shembulli
2 : Gjeni vlerën e \(\cos(5\pi/2)\)
Zgjidhja: \(\cos(5\pi/2) = \cos (2\pi + {1\pi}/_2)\)
Ndërsa vlera e kosinusit përsëritet pas \(2\pi \) prandaj, \(\cos(2\pi + {1\pi}/_2) = \cos(\pi/2) = 0\)