Eftersom vi vet hur man mäter en spetsig vinkel för den räta triangeln som förhållandet mellan dess sidor, är det dags att lära sig trigonometriska förhållande till vilken vinkel som helst i termer av radianmått och studera dem som trigonometriska funktioner.
Betrakta en cirkel med enhetsradie, vars centrum är vid koordinataxlarnas ursprung.
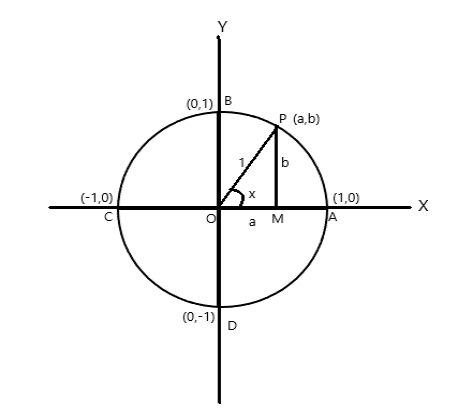
Koordinatpunkter för A = (1,0), B = (0,1), C = (-1,0) och D = (0,-1)
Låt P (a,b) vara vilken punkt som helst på cirkeln med \(\angle AOP = x \) radian. Därför längden på bågen \(AP = x \) enhet.
\(\cos x = a\) , \(\sin x = b\) . Eftersom \(\bigtriangleup POM\) är en rätvinklig triangel, \(OP^2 = OM^2 + PM^2\)
därför \(1 = a^2 + b^2\)
| \(\mathbf{ \cos^2 x + \sin^2x = 1}\) |
Eftersom ett fullständigt varv underför cirkelns mitt en vinkel på \(2\pi\) radian. Från ovanstående figur
\(\angle AOB = \pi/2 \)
\(\angle AOC = \pi\)
\(\angle AOD = \frac{3\pi}{2} \)
Vi vet \(\cos x = \frac {\textrm {Base}}{\textrm{Hypotenuse}}\) och \(\sin x = \frac {\textrm {Perpendicular}}{\textrm{Hypotenuse}}\)
\(\cos0^\circ = 1\) \(\sin0^\circ = 0\)
\(\cos\frac{\pi}{2} = 0\) \(\sin\frac{\pi}{2} = 1\)
\(\cos\pi = -1\) \(\sin\pi = 0\)
\(\cos2\pi = 1\) \(\sin2\pi = 0\)
När vi tar ett helt varv från punkt P når vi punkt P igen. Värdet på \(\cos x\) och \(\sin x\) förblir detsamma, därför kan vi säga att
när x ökar eller minskar med en heltalsmultipel av \(2\pi\) ändras inte värdet på sinus, cosinusfunktionen. Således,
\(\sin(n\cdot2\pi + x) = \sin x\)
\(\cos(n\cdot 2\pi + x) = \cos x \)
där n är ett heltal.
Vi kommer att märka att \(\sin x = 0\) när \(\space x = n\pi\)
och \(\cos x = 0\) när \(x = (2n+1)\pi/2\)
Härleda andra trigonometriska funktioner i termer av sinus- och cosinusfunktioner.
| \(\mathbf{\csc x} = \mathbf{\frac{1}{\sin x}}\) där \(x \neq n\pi\) |
| \(\mathbf{\sec x } = \mathbf{\frac{1}{\cos x}}\) där |
| \(\mathbf{\tan x } = \mathbf{\frac{\sin x}{\cos x}}\) där |
| \(\mathbf{\cot x } = \mathbf{\frac{\cos x}{\sin x}}\) där \( x \neq n\pi\) |
| \(\textbf 1 + \mathbf {\tan^2x = \sec^2x}\) |
| \(\textbf 1 + \mathbf {\cot^2x = \csc^2x}\) |
Tabellen nedan visar hur tecknet och värdet för trigonometriska funktioner förändras i olika kvadranter.
| Kvadranter | I | II | III | IV |
| sinx | + | + | − | − |
| cosx | + | − | − | + |
| tanx | + | − | + | − |
| cosecx | + | + | − | − |
| secx | + | − | − | + |
| cotx | + | − | + | − |
Ta en titt på tabellen nedan som visar värdet av trigonometriska vinklar för grader som 0°, 30°, 45°, 60° och 90°.
Vinklar (i grader & radianer) | sin | cot | tan | cot | csc | sek |
| 0° | 0 | 1 | 0 | ∞ | ∞ | 1 |
| 30° eller π/6 radian | 1/2 | √3/2 | 1/√3 | √3 | 2 | 2/√3 |
| 45 ° eller π/4 radian | 1/√2 | 1/√2 | 1 | 1 | √2 | √2 |
| 60° eller π/3 radian | √3/2 | 1/2 | √3 | 1/ √3 | 2/√3 | 2 |
| 90° eller π/2 radian | 1 | 0 | ∞ | 0 | 1 | ∞ |
| 180° eller π radian | 0 | -1 | 0 | ∞ | ∞ | -1 |
| 270° eller 3π/2 radian | -1 | 0 | ∞ | 0 | - 1 | ∞ |
| 360° eller 2π radian | 0 | 1 | 0 | ∞ | ∞ | 1 |
Observera tabellen ovan, du kommer att märka att:
( \mathbf{\tan x = \cot(90^\circ\(\mathbf{\sin x = \cos(90^\circ-x)}\) |
| \(\mathbf{\tan x = \cot(90^\circ-x)}\) |
| \(\mathbf{\tan x = \cot(90^\circ-x)}\) |
| \(\mathbf{\sec x = \csc(90^\circ-x) }\) |
| \(\mathbf{\csc x = \sec(90^\circ-x)}\) |
| \( \mathbf{ \sin(-x) = -\sin x}\) |
| \( \mathbf{ \cos(-x) = \cos x}\) |
| \(\tan(-x) = -\tan x\) |
Grafisk representation av \(\sin x\) och \(\cos x\) där y sträcker sig från -1 till +1 när x tar värden från \(-3\pi \) till \(3\pi \) . Både sinus- och cosinusvärden för trigonometriska funktioner upprepas efter ett intervall på \(2\pi \) .
Sinus visas som en heldragen linje och Cosinus som en prickad linje.
Låt oss lösa några exempel baserat på ovanstående trigonometriska funktioner:
Exempel 1: Om \(\cos x\) = − 4/5, x ligger i den tredje kvadranten, hitta värdena för de andra fem trigonometriska funktionerna.
Lösning: Se tabellerna ovan.
Som \(\cos x\) = -4/5, därför \(\sec x\) = -5/4
Som \(\mathbf{ \cos^2 x + \sin^2x = 1}\) så \({16\over25} + \sin^2x = 1 ⇒ \sin^2x = 1-\frac{16}{25} = {9\over25}\)
\(\sin x = \pm3/5\)
Eftersom x ligger i tredje kvadrantvärdet, så kommer \(\sin x\) att vara negativ (se tabellen för kvadranttecken). Därför \(\sin x\) = -3/5 och \(\csc x \) = -5/3
Som \(\tan x = \sin x/\cos x\) , därför \(\tan x\) = \(\frac{-4/5}{-3/5}\) = 4/3 Exempel
2 : Hitta värdet för \(\cos(5\pi/2)\)
Lösning: \(\cos(5\pi/2) = \cos (2\pi + {1\pi}/_2)\)
Eftersom värdet för cosinus upprepas efter \(2\pi \) därför \(\cos(2\pi + {1\pi}/_2) = \cos(\pi/2) = 0\)