Back to the topics list

kazi za trigonometric

Kama tunavyojua jinsi ya kupima pembe kali ya pembetatu ya kulia kama uwiano wa pande zake, ni wakati wa kujifunza uwiano wa trigonometriki kwa pembe yoyote kulingana na kipimo cha radian na kuzisoma kama vitendaji vya trigonometric.

Fikiria mduara wa radius ya kitengo, ambayo katikati iko kwenye asili ya shoka za kuratibu.

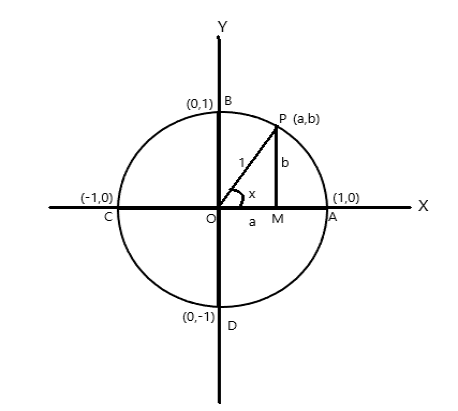
Kuratibu pointi za A = (1,0), B = (0,1), C = (-1,0) na D = (0,-1)
Acha P (a,b) iwe sehemu yoyote kwenye duara yenye \(\angle AOP = x \) radian. Kwa hivyo urefu wa arc \(AP = x \) kitengo.
\(\cos x = a\) , \(\sin x = b\) . Kama \(\bigtriangleup POM\) ni pembetatu ya kulia, \(OP^2 = OM^2 + PM^2\)
kwa hivyo \(1 = a^2 + b^2\) ⇒

Kwa kuwa mapinduzi moja kamili huteremsha katikati ya duara pembe ya \(2\pi\) radian. Kutoka kwa takwimu hapo juu
\(\angle AOB = \pi/2 \)
\(\angle AOC = \pi\)
\(\angle AOD = \frac{3\pi}{2} \)
Tunajua \(\cos x = \frac {\textrm {Base}}{\textrm{Hypotenuse}}\) na \(\sin x = \frac {\textrm {Perpendicular}}{\textrm{Hypotenuse}}\)
\(\cos0^\circ = 1\) \(\sin0^\circ = 0\)
\(\cos\frac{\pi}{2} = 0\) \(\sin\frac{\pi}{2} = 1\)
\(\cos\pi = -1\) \(\sin\pi = 0\)
\(\cos2\pi = 1\) \(\sin2\pi = 0\)

Tunapochukua mapinduzi moja kamili kutoka kwa nukta P tunafikia tena hatua ya P. Thamani ya \(\cos x\) na \(\sin x\) inabaki vile vile, kwa hivyo tunaweza kusema kwamba.
x inapoongezeka au kupungua kwa kizidishio muhimu cha \(2\pi\) , thamani ya sine, kitendakazi cha kosine haibadiliki. Hivyo,

\(\sin(n\cdot2\pi + x) = \sin x\)

\(\cos(n\cdot 2\pi + x) = \cos x \)
ambapo n ni nambari kamili.
Tutagundua kuwa \(\sin x = 0\) wakati \(\space x = n\pi\)
na \(\cos x = 0\) wakati \(x = (2n+1)\pi/2\)

Kutoa utendaji mwingine wa trigonometric katika suala la utendaji wa sine na kosini.

Kwa kutumia \(\cos^2 x + \sin^2x = 1\) tunaweza kupata fomula zilizo hapa chini:

Ishara ya Kazi za Trigonometric

Jedwali lililo hapa chini linaonyesha jinsi ishara na thamani ya vitendaji vya trigonometric hubadilika katika roboduara tofauti.

Angalia jedwali lililo hapa chini linaloonyesha thamani ya pembe tatu kwa digrii kama vile 0°, 30°, 45°, 60° na 90°.

Angalia jedwali hapo juu, utagundua kuwa:

Uwakilishi wa mchoro wa \(\sin x\) na \(\cos x\) ambapo y huanzia -1 hadi +1 wakati x inachukua thamani kutoka \(-3\pi \) hadi \(3\pi \) . Thamani zote mbili za chaguo za kukokotoa za trigonometric sine na cosine hurudia baada ya muda \(2\pi \) .

Sine inaonyeshwa kama mstari thabiti na Cosine kama mstari wa nukta.

Wacha tusuluhishe mifano michache kulingana na kazi za trigonometric hapo juu:

Mfano 1: Ikiwa \(\cos x\) = - 4/5, x iko katika roboduara ya tatu, tafuta maadili ya vitendakazi vingine vitano vitano.

Suluhisho: Rejelea majedwali yaliyotolewa hapo juu.
Kama \(\cos x\) = -4/5, kwa hivyo \(\sec x\) = -5/4
Kama \(\mathbf{ \cos^2 x + \sin^2x = 1}\) hivyo \({16\over25} + \sin^2x = 1 ⇒ \sin^2x = 1-\frac{16}{25} = {9\over25}\)
\(\sin x = \pm3/5\)
Kama x iko katika thamani ya roboduara ya tatu, kwa hivyo \(\sin x\) itakuwa hasi(rejelea jedwali la ishara ya roboduara). Kwa hiyo \(\sin x\) = -3/5 na \(\csc x \) = -5/3
Kama \(\tan x = \sin x/\cos x\) , kwa hivyo \(\tan x\) = \(\frac{-4/5}{-3/5}\) = 4/3

Mfano wa 2: Tafuta thamani ya \(\cos(5\pi/2)\)
Suluhisho:   \(\cos(5\pi/2) = \cos (2\pi + {1\pi}/_2)\)
Kama thamani ya cosine inavyojirudia baada ya \(2\pi \) kwa hivyo \(\cos(2\pi + {1\pi}/_2) = \cos(\pi/2) = 0\)