เมื่อเรารู้วิธีวัดมุมแหลมสำหรับสามเหลี่ยมมุมฉากเป็นอัตราส่วนของด้านแล้ว ก็ถึงเวลาเรียนรู้อัตราส่วนตรีโกณมิติต่อมุมใดๆ ในแง่ของการวัดเรเดียน และศึกษาพวกมันในรูปของฟังก์ชันตรีโกณมิติ
พิจารณาวงกลมหน่วยรัศมี ซึ่งจุดศูนย์กลางอยู่ที่แกนพิกัดจุดกำเนิด
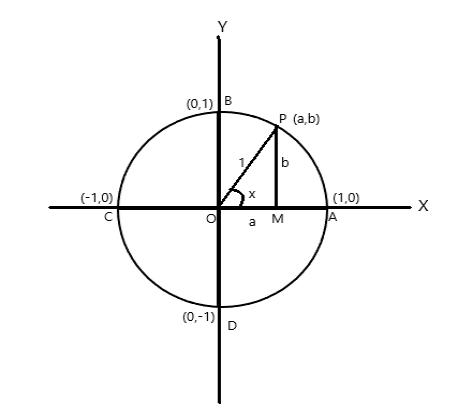
จุดพิกัดของ A = (1,0), B = (0,1), C = (-1,0) และ D = (0,-1)
ให้ P (a,b) เป็นจุดใดๆ บนวงกลมที่มี \(\angle AOP = x \) เรเดียน ดังนั้นความยาวของส่วนโค้ง \(AP = x \) หน่วย
\(\cos x = a\) , \(\sin x = b\) เนื่องจาก \(\bigtriangleup POM\) เป็นสามเหลี่ยมมุมฉาก \(OP^2 = OM^2 + PM^2\)
ดังนั้น \(1 = a^2 + b^2\)
| \(\mathbf{ \cos^2 x + \sin^2x = 1}\) |
เนื่องจากการปฏิวัติที่สมบูรณ์หนึ่งครั้งจะตัดมุม \(2\pi\) เรเดียนที่จุดศูนย์กลางของวงกลม จากรูปด้านบน
\(\angle AOB = \pi/2 \)
\(\angle AOC = \pi\)
\(\angle AOD = \frac{3\pi}{2} \)
เรารู้ \(\cos x = \frac {\textrm {Base}}{\textrm{Hypotenuse}}\) และ \(\sin x = \frac {\textrm {Perpendicular}}{\textrm{Hypotenuse}}\)
\(\cos0^\circ = 1\) \(\sin0^\circ = 0\)
\(\cos\frac{\pi}{2} = 0\) \(\sin\frac{\pi}{2} = 1\)
\(\cos\pi = -1\) \(\sin\pi = 0\)
\(\cos2\pi = 1\) \(\sin2\pi = 0\)
เมื่อเราหมุนครบหนึ่งรอบจากจุด P เราก็ไปถึงจุด P อีกครั้ง ค่าของ \(\cos x\) และ \(\sin x\) ยังคงเท่าเดิม ด้วยเหตุนี้เราจึงกล่าวได้ว่า
เมื่อ x เพิ่มขึ้นหรือลดลงโดยการคูณอินทิกรัลของ \(2\pi\) ค่าของไซน์ ฟังก์ชันโคไซน์จะไม่เปลี่ยนแปลง ดังนั้น,
\(\sin(n\cdot2\pi + x) = \sin x\)
\(\cos(n\cdot 2\pi + x) = \cos x \)
โดยที่ n เป็นจำนวนเต็ม
เราจะสังเกตว่า \(\sin x = 0\) เมื่อ \(\space x = n\pi\)
และ \(\cos x = 0\) เมื่อ \(x = (2n+1)\pi/2\)
หาฟังก์ชันตรีโกณมิติอื่น ๆ ในรูปของฟังก์ชันไซน์และโคไซน์
| \(\mathbf{\csc x} = \mathbf{\frac{1}{\sin x}}\) โดยที่ \(x \neq n\pi\) |
| \(\mathbf{\sec x } = \mathbf{\frac{1}{\cos x}}\) โดยที่ |
| \(\mathbf{\tan x } = \mathbf{\frac{\sin x}{\cos x}}\) โดยที่ |
| \(\mathbf{\cot x } = \mathbf{\frac{\cos x}{\sin x}}\) โดยที่ \( x \neq n\pi\) |
| \(\textbf 1 + \mathbf {\tan^2x = \sec^2x}\) |
| \(\textbf 1 + \mathbf {\cot^2x = \csc^2x}\) |
ตารางด้านล่างแสดงการเปลี่ยนแปลงของเครื่องหมายและค่าของฟังก์ชันตรีโกณมิติในควอแดรนต์ต่างๆ
| จตุภาค | ฉัน | ครั้งที่สอง | สาม | IV |
| บาป | + | + | - | - |
| คอสเอ็กซ์ | + | - | - | + |
| แทนซ์ | + | - | + | - |
| โคเซก | + | + | - | - |
| วินาที | + | - | - | + |
| คอทซ์ | + | - | + | - |
ดูตารางด้านล่างซึ่งแสดงค่าของมุมตรีโกณมิติสำหรับองศาต่างๆ เช่น 0°, 30°, 45°, 60° และ 90°
มุม (เป็นองศาและเรเดียน) | บาป | เพราะ | ผิวสีแทน | เปล | ก.พ | วินาที |
| 0° | 0 | 1 | 0 | ∞ | ∞ | 1 |
| 30° หรือ π/6 เรเดียน | 1/2 | √3/2 | 1/√3 | √3 | 2 | 2/√3 |
| 45° หรือ π/4 เรเดียน | 1/√2 | 1/√2 | 1 | 1 | √2 | √2 |
| 60° หรือ π/3 เรเดียน | √3/2 | 1/2 | √3 | 1/√3 | 2/√3 | 2 |
| 90° หรือ π/2 เรเดียน | 1 | 0 | ∞ | 0 | 1 | ∞ |
| 180° หรือ π เรเดียน | 0 | -1 | 0 | ∞ | ∞ | -1 |
| 270° หรือ 3π/2 เรเดียน | -1 | 0 | ∞ | 0 | -1 | ∞ |
| 360° หรือ 2π เรเดียน | 0 | 1 | 0 | ∞ | ∞ | 1 |
สังเกตตารางด้านบน คุณจะสังเกตเห็นว่า:
\(\mathbf{\sin x = \cos(90^\circ-x)}\) |
| \(\mathbf{\tan x = \cot(90^\circ-x)}\) |
| \(\mathbf{\sec x = \csc(90^\circ-x) }\) |
| \(\mathbf{\csc x = \sec(90^\circ-x)}\) |
| \( \mathbf{ \sin(-x) = -\sin x}\) |
| \( \mathbf{ \cos(-x) = \cos x}\) |
| \(\tan(-x) = -\tan x\) |
การแสดงกราฟิกของ \(\sin x\) และ \(\cos x\) โดยที่ y มีช่วงตั้งแต่ -1 ถึง +1 เมื่อ x รับค่าจาก \(-3\pi \) ถึง \(3\pi \) ทั้งฟังก์ชันตรีโกณมิติ ค่าไซน์และโคไซน์จะทำซ้ำหลังจากช่วงเวลา \(2\pi \)
ไซน์แสดงเป็นเส้นทึบและโคไซน์เป็นเส้นประ
ให้เราแก้ตัวอย่างตามฟังก์ชันตรีโกณมิติด้านบน:
ตัวอย่างที่ 1: ถ้า \(\cos x\) = − 4/5, x อยู่ในจตุภาคที่สาม ให้หาค่าของฟังก์ชันตรีโกณมิติอีกห้าฟังก์ชันที่เหลือ
วิธีแก้ไข: อ้างอิงจากตารางที่ให้ไว้ด้านบน
เนื่องจาก \(\cos x\) = -4/5 ดังนั้น \(\sec x\) = -5/4
เนื่องจาก \(\mathbf{ \cos^2 x + \sin^2x = 1}\) ดังนั้น \({16\over25} + \sin^2x = 1 ⇒ \sin^2x = 1-\frac{16}{25} = {9\over25}\)
\(\sin x = \pm3/5\)
เนื่องจาก x อยู่ในค่าจตุภาคที่สาม ดังนั้น \(\sin x\) จะเป็นค่าลบ (อ้างอิงจากตารางเครื่องหมายจตุภาค) ดังนั้น \(\sin x\) = -3/5 และ \(\csc x \) = -5/3
เนื่องจาก \(\tan x = \sin x/\cos x\) ดังนั้น \(\tan x\) = \(\frac{-4/5}{-3/5}\) = 4/3
ตัวอย่างที่ 2: หาค่าของ \(\cos(5\pi/2)\)
สารละลาย: \(\cos(5\pi/2) = \cos (2\pi + {1\pi}/_2)\)
เนื่องจากค่าโคไซน์ซ้ำหลังจาก \(2\pi \) ดังนั้น \(\cos(2\pi + {1\pi}/_2) = \cos(\pi/2) = 0\)