Tulad ng alam natin kung paano sukatin ang isang matinding anggulo para sa tamang tatsulok bilang ratio ng mga gilid nito, oras na upang matutunan ang mga trigonometric ratio sa anumang anggulo sa mga tuntunin ng radian measure at pag-aralan ang mga ito bilang mga function ng trigonometriko.
Isaalang-alang ang isang bilog ng unit radius, na ang sentro ay nasa coordinate axes na pinanggalingan.
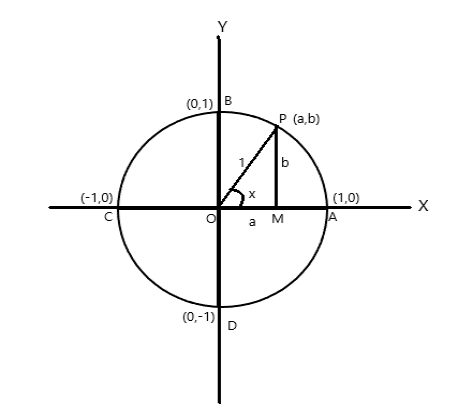
Mga coordinate na puntos ng A = (1,0), B = (0,1), C = (-1,0) at D = (0,-1)
Hayaan ang P (a,b) maging anumang punto sa bilog na may \(\angle AOP = x \) radian. Samakatuwid ang haba ng arc \(AP = x \) unit.
\(\cos x = a\) , \(\sin x = b\) . Dahil ang \(\bigtriangleup POM\) ay isang right-angle triangle, \(OP^2 = OM^2 + PM^2\)
samakatuwid \(1 = a^2 + b^2\)
| \(\mathbf{ \cos^2 x + \sin^2x = 1}\) |
Dahil ang isang kumpletong rebolusyon ay nag-subtend sa gitna ng bilog ng isang anggulo ng \(2\pi\) radian. Mula sa figure sa itaas
\(\angle AOB = \pi/2 \)
\(\angle AOC = \pi\)
\(\angle AOD = \frac{3\pi}{2} \)
Alam natin \(\cos x = \frac {\textrm {Base}}{\textrm{Hypotenuse}}\) at \(\sin x = \frac {\textrm {Perpendicular}}{\textrm{Hypotenuse}}\)
\(\cos0^\circ = 1\) \(\sin0^\circ = 0\)
\(\cos\frac{\pi}{2} = 0\) \(\sin\frac{\pi}{2} = 1\)
\(\cos\pi = -1\) \(\sin\pi = 0\)
\(\cos2\pi = 1\) \(\sin2\pi = 0\)
Habang kumukuha tayo ng isang kumpletong rebolusyon mula sa puntong P muli nating narating ang puntong P. Ang halaga ng \(\cos x\) at \(\sin x\) ay nananatiling pareho, kaya masasabi natin na
habang ang x ay tumataas o bumababa ng isang integral multiple ng \(2\pi\) , ang halaga ng sine, cosine function ay hindi nagbabago. kaya,
\(\sin(n\cdot2\pi + x) = \sin x\)
\(\cos(n\cdot 2\pi + x) = \cos x \)
kung saan ang n ay isang integer.
Mapapansin natin na \(\sin x = 0\) kapag \(\space x = n\pi\)
at \(\cos x = 0\) kapag \(x = (2n+1)\pi/2\)
Pagkuha ng iba pang trigonometric function sa mga tuntunin ng sine at cosine function.
| \(\mathbf{\csc x} = \mathbf{\frac{1}{\sin x}}\) kung saan \(x \neq n\pi\) |
| \(\mathbf{\sec x } = \mathbf{\frac{1}{\cos x}}\) kung saan |
| \(\mathbf{\tan x } = \mathbf{\frac{\sin x}{\cos x}}\) kung saan |
| \(\mathbf{\cot x } = \mathbf{\frac{\cos x}{\sin x}}\) kung saan \( x \neq n\pi\) |
| \(\textbf 1 + \mathbf {\tan^2x = \sec^2x}\) |
| \(\textbf 1 + \mathbf {\cot^2x = \csc^2x}\) |
Ipinapakita ng talahanayan sa ibaba kung paano nagbabago ang tanda at halaga ng mga function ng trigonometriko sa iba't ibang mga quadrant.
| Quadrants | I | II | III | IV |
| sinx | + | + | − | − |
| cosx | + | − | − | + |
| tanx | + | − | + | − |
| cosecx | + | + | − | − |
| secx | + | − | − | + |
| cotx | + | − | + | − |
Tingnan ang talahanayan sa ibaba na nagpapakita ng halaga ng mga trigonometrikong anggulo para sa mga digri gaya ng 0°, 30°, 45°, 60°, at 90°.
Mga anggulo(sa degrees at radian) | sin | cos | tan | cot | csc | sec |
| 0° | 0 | 1 | 0 | ∞ | ∞ | 1 |
| 30° o π/6 radian | 1/2 | √3/2 1/ | √3 √3 | 2 | 2 | /√3 |
| 45 | ° o π/4 radian | 1/ √2 | 1 | √2 | √2 | 2 |
| / | 2 | radian | 1 0 ∞ 0 | 1 | ∞ 180° | |
| π | radian | 0 | -1 | 0 | ∞ | |
| ∞ | -1 | 270 | ° | o | ➈3π | / |
| 0 | ∞ | 3π | / | 0 | ∞ | π |
| radian | 0 | 1 | 0 | ∞ | ∞ | 1 |
Obserbahan ang talahanayan sa itaas, mapapansin mo na:
{\tan x Graphical na representasyon ng \(\sin x\) at \(\cos x\) kung saan ang y ay mula -1 hanggang +1(-) kapag ang x ay kumukuha ng mga value mula sa \)(-(-\(\mathbf{\sin x = \cos(90^\circ-x)}\) |
| \(\mathbf{\tan x = \cot(90^\circ-x)}\) |
| \(\mathbf{\sec x = \csc(90^\circ-x) }\) |
| \(\mathbf{\csc x = \sec(90^\circ-x)}\) |
| \( \mathbf{ \sin(-x) = -\sin x}\) |
| \( \mathbf{ \cos(-x) = \cos x}\) |
| \(\tan(-x) = -\tan x\) |
\(\sin x\) \(\cos x\) \(-3\pi \) \(3\pi \) Ang parehong trigonometric function na mga halaga ng sine at cosine ay umuulit pagkatapos ng pagitan ng \(2\pi \) .
Ang Sine ay ipinapakita bilang isang solidong linya at ang Cosine bilang isang tuldok na linya.
Lutasin natin ang ilang halimbawa batay sa itaas na trigonometriko function:
Halimbawa 1: Kung \(\cos x\) = − 4/5, x ay nasa ikatlong kuwadrante, hanapin ang mga halaga ng iba pang limang trigonometric function.
Solusyon: Sumangguni sa mga talahanayan na ibinigay sa itaas.
Bilang \(\cos x\) = -4/5, samakatuwid \(\sec x\) = -5/4
Bilang \(\mathbf{ \cos^2 x + \sin^2x = 1}\) \({16\over25} + \sin^2x = 1 ⇒ \sin^2x = 1-\frac{16}{25} = {9\over25}\)
\(\sin x = \pm3/5\)
Dahil ang x ay nasa ikatlong kuwadrante na halaga, kaya \(\sin x\) ay magiging negatibo (sumangguni sa talahanayan ng tanda ng kuwadrante). Samakatuwid \(\sin x\) = -3/5 at \(\csc x \) = -5/3
Bilang \(\tan x = \sin x/\cos x\) , samakatuwid \(\tan x\) = \(\frac{-4/5}{-3/5}\) = 4/3 Halimbawa 2: Hanapin ang halaga ng \(\cos(5\pi/2)\
\(\cos(5\pi/2)\)
Solusyon: \(\cos(5\pi/2) = \cos (2\pi + {1\pi}/_2)\)
Habang umuulit ang halaga ng cosine pagkatapos ng \(2\pi \) samakatuwid, \(\cos(2\pi + {1\pi}/_2) = \cos(\pi/2) = 0\)