Back to the topics list
Google Play badge

trigonometrik fonksiyonlar

Dik üçgen için bir dar açıyı kenarlarının oranı olarak nasıl ölçeceğimizi bildiğimize göre, herhangi bir açının trigonometrik oranlarını radyan ölçüsü cinsinden öğrenmenin ve bunları trigonometrik fonksiyonlar olarak incelemenin zamanı geldi.

Merkezi koordinat eksenlerinin başlangıç ​​noktasında olan birim yarıçaplı bir daire düşünün.


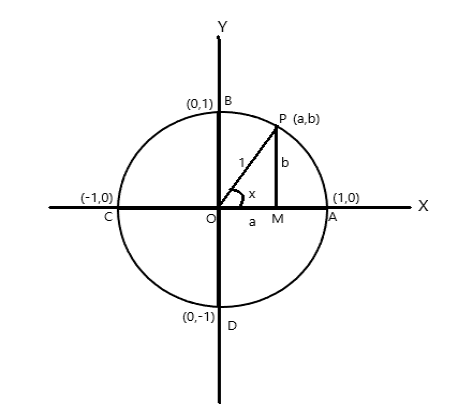
A = (1,0), B = (0,1), C = (-1,0) ve D = (0,-1) koordinat noktaları
P(a,b) daire üzerinde \(\angle AOP = x \) radyan olan herhangi bir nokta olsun. Bu nedenle yay uzunluğu \(AP = x \) birimidir.
\(\cos x = a\) , \(\sin x = b\) . \(\bigtriangleup POM\) bir dik açılı üçgen olduğundan, \(OP^2 = OM^2 + PM^2\)
dolayısıyla \(1 = a^2 + b^2\) ⇒

\(\mathbf{ \cos^2 x + \sin^2x = 1}\)

Bir tam devir dairenin merkezinde \(2\pi\) radyanlık bir açı oluşturduğundan. Yukarıdaki şekilden
\(\angle AOB = \pi/2 \)
\(\angle AOC = \pi\)
\(\angle AOD = \frac{3\pi}{2} \)
\(\cos x = \frac {\textrm {Base}}{\textrm{Hypotenuse}}\) ve \(\sin x = \frac {\textrm {Perpendicular}}{\textrm{Hypotenuse}}\) biliyoruz. \(\sin x = \frac {\textrm {Perpendicular}}{\textrm{Hypotenuse}}\)
\(\cos0^\circ = 1\) \(\sin0^\circ = 0\)
\(\cos\frac{\pi}{2} = 0\) \(\sin\frac{\pi}{2} = 1\)
\(\cos\pi = -1\) \(\sin\pi = 0\)
\(\cos2\pi = 1\) \(\sin2\pi = 0\)

P noktasından bir tam devir aldığımızda tekrar P noktasına ulaşırız \(\cos x\) ve \(\sin x\) değerleri aynı kalır, dolayısıyla şunu söyleyebiliriz:
x \(2\pi\) nin tam katı kadar artarken veya azalırken, sinüs, kosinüs fonksiyonunun değeri değişmez. Böylece,

\(\sin(n\cdot2\pi + x) = \sin x\)

\(\cos(n\cdot 2\pi + x) = \cos x \)
burada n bir tamsayıdır.
\(\space x = n\pi\) olduğunda \(\sin x = 0\) olduğunu fark edeceğiz.
ve \(\cos x = 0\) olduğunda \(x = (2n+1)\pi/2\)

Sinüs ve kosinüs fonksiyonları cinsinden diğer trigonometrik fonksiyonların türetilmesi.

\(\mathbf{\csc x} = \mathbf{\frac{1}{\sin x}}\) burada \(x \neq n\pi\)
\(\mathbf{\sec x } = \mathbf{\frac{1}{\cos x}}\) burada \( x \neq (2n+1)\frac{\pi}{2}\)
\(\mathbf{\tan x } = \mathbf{\frac{\sin x}{\cos x}}\) burada \(x \neq (2n+1)\frac{\pi}{2}\)
\(\mathbf{\cot x } = \mathbf{\frac{\cos x}{\sin x}}\) burada \( x \neq n\pi\)

\(\cos^2 x + \sin^2x = 1\) kullanarak aşağıdaki formülleri türetebiliriz:

\(\textbf 1 + \mathbf {\tan^2x = \sec^2x}\)
\(\textbf 1 + \mathbf {\cot^2x = \csc^2x}\)
Trigonometrik Fonksiyonların İşareti

Aşağıdaki tablo, trigonometrik fonksiyonların işaretinin ve değerinin farklı kadranlarda nasıl değiştiğini göstermektedir.

Çeyrekler BEN III III IV
sinx + + - -
cosx + - - +
tanks + - + -
cosecx + + - -
seks + - - +
karyola + - + -

0°, 30°, 45°, 60° ve 90° gibi dereceler için trigonometrik açıların değerini gösteren aşağıdaki tabloya bakın.

Açılar(derece ve radyan cinsinden)

 günah çünkü bronzlaşmak karyola csc saniye
0° 0 1 0 ∞ ∞ 1
30° veya π/6 radyan 1/2 ​√3/2 1/√3 √3 2 2/√3
45° veya π/4 radyan 1/√2 1/√2 1 1 √2 √2
60° veya π/3 radyan​ ​ √3/2 1/2 ​​√3 1/√3 ​2/√3​ 2
90° veya π/2 radyan 1 0​ ∞ ​0 1 ∞
180° veya π radyan 0 -1 0 ∞ ∞ -1
270° veya 3π/2 radyan -1 0 ∞ 0 -1 ∞
360° veya 2π radyan 0 1 0 ∞ ∞ 1

Yukarıdaki tabloya bakın, şunu fark edeceksiniz:

\(\mathbf{\sin x = \cos(90^\circ-x)}\)

\(\mathbf{\tan x = \cot(90^\circ-x)}\)
\(\mathbf{\sec x = \csc(90^\circ-x) }\)
\(\mathbf{\csc x = \sec(90^\circ-x)}\)
\( \mathbf{ \sin(-x) = -\sin x}\)
\( \mathbf{ \cos(-x) = \cos x}\)
\(\tan(-x) = -\tan x\)

\(\sin x\) \(-3\pi \) ila \ \(3\pi \) arasında değer aldığında y'nin -1 ile +1 arasında değiştiği \(\sin x\) ve \(\cos x\) 'nin grafik gösterimi. Hem trigonometrik fonksiyon sinüs hem de kosinüs değerleri \(2\pi \) aralığından sonra tekrarlanır.


Sinüs düz çizgi ve Kosinüs noktalı çizgi olarak gösterilir.

Yukarıdaki trigonometrik fonksiyonlara dayalı birkaç örnek çözelim:


Örnek 1: Eğer \(\cos x\) = − 4/5, x üçüncü kadranda yer alıyorsa, diğer beş trigonometrik fonksiyonun değerlerini bulun.

Çözüm: Yukarıda verilen tablolara bakın.
\(\cos x\) = -4/5 olduğundan, \(\sec x\) = -5/4
\(\mathbf{ \cos^2 x + \sin^2x = 1}\) olduğundan, yani \({16\over25} + \sin^2x = 1 ⇒ \sin^2x = 1-\frac{16}{25} = {9\over25}\)
\(\sin x = \pm3/5\)
x, üçüncü kadran değerinde yer aldığından \(\sin x\) negatif olacaktır (çeyrek işaret tablosuna bakın). Bu nedenle \(\sin x\) = -3/5 ve \(\csc x \) = -5/3
\(\tan x = \sin x/\cos x\) olduğundan \(\tan x\) = \(\frac{-4/5}{-3/5}\) = 4/3

Örnek 2: \(\cos(5\pi/2)\) değerini bulun
Çözüm:   \(\cos(5\pi/2) = \cos (2\pi + {1\pi}/_2)\)
Kosinüs değeri \(2\pi \) den sonra tekrar ettiği için, \(\cos(2\pi + {1\pi}/_2) = \cos(\pi/2) = 0\)

Download Primer to continue