Оскільки ми знаємо, як виміряти гострий кут прямокутного трикутника як відношення його сторін, настав час вивчити тригонометричні співвідношення до будь-якого кута в термінах радіанної міри та вивчати їх як тригонометричні функції.
Розглянемо коло одиничного радіуса, центр якого знаходиться в початку координатних осей.
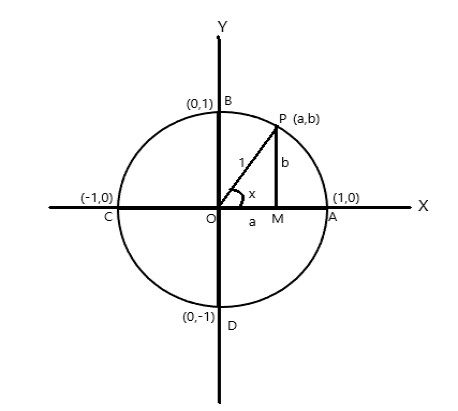
Координати точок A = (1,0), B = (0,1), C = (-1,0) і D = (0,-1)
Нехай P (a,b) — будь-яка точка на колі з \(\angle AOP = x \) радіан. Тому довжина дуги \(AP = x \) од.
\(\cos x = a\) , \(\sin x = b\) . Оскільки \(\bigtriangleup POM\) є прямокутним трикутником, \(OP^2 = OM^2 + PM^2\)
тому \(1 = a^2 + b^2\)
| \(\mathbf{ \cos^2 x + \sin^2x = 1}\) |
Оскільки один повний оберт утворює в центрі кола кут \(2\pi\) радіан. З наведеного вище малюнка
\(\angle AOB = \pi/2 \)
\(\angle AOC = \pi\)
\(\angle AOD = \frac{3\pi}{2} \)
Ми знаємо \(\cos x = \frac {\textrm {Base}}{\textrm{Hypotenuse}}\) і \(\sin x = \frac {\textrm {Perpendicular}}{\textrm{Hypotenuse}}\)
\(\cos0^\circ = 1\) \(\sin0^\circ = 0\)
\(\cos\frac{\pi}{2} = 0\) \(\sin\frac{\pi}{2} = 1\)
\(\cos\pi = -1\) \(\sin\pi = 0\)
\(\cos2\pi = 1\) \(\sin2\pi = 0\)
Коли ми зробимо один повний оберт від точки P, ми знову досягнемо точки P. Значення \(\cos x\) і \(\sin x\) залишаються незмінними, тому ми можемо сказати, що
коли х збільшується або зменшується на ціле число \(2\pi\) , значення функції синус, косинус не змінюється. Таким чином,
\(\sin(n\cdot2\pi + x) = \sin x\)
\(\cos(n\cdot 2\pi + x) = \cos x \)
де n - ціле число.
Ми помітимо, що \(\sin x = 0\) коли \(\space x = n\pi\)
і \(\cos x = 0\) коли \(x = (2n+1)\pi/2\)
Отримання інших тригонометричних функцій через функції синусів і косинусів.
| \(\mathbf{\csc x} = \mathbf{\frac{1}{\sin x}}\) де \(x \neq n\pi\) |
| \(\mathbf{\sec x } = \mathbf{\frac{1}{\cos x}}\) де |
| \(\mathbf{\tan x } = \mathbf{\frac{\sin x}{\cos x}}\) де |
| \(\mathbf{\cot x } = \mathbf{\frac{\cos x}{\sin x}}\) де \( x \neq n\pi\) |
| \(\textbf 1 + \mathbf {\tan^2x = \sec^2x}\) |
| \(\textbf 1 + \mathbf {\cot^2x = \csc^2x}\) |
У таблиці нижче показано, як змінюються знак і значення тригонометричних функцій у різних квадрантах.
| Квадранти | я | II | III | IV |
| sinx | + | + | − | − |
| cosx | + | − | − | + |
| tanx | + | − | + | − |
| cosecx | + | + | − | − |
| secx | + | − | − | + |
| cotx | + | − | + | − |
Подивіться на наведену нижче таблицю, яка показує значення тригонометричних кутів для таких градусів, як 0°, 30°, 45°, 60° і 90°.
Кути (в градусах і радіанах) | гріх | cos | загар | ліжечко | csc | сек |
| 0° | 0 | 1 | 0 | ∞ | ∞ | 1 |
| 30° або π/6 радіан | 1/2 | √3/2 | 1/√3 | √3 | 2 | 2/√3 |
| 45° або π/4 радіана | 1/√2 | 1/√2 | 1 | 1 | √2 | √2 |
| 60° або π/3 радіана | √3/2 | 1/2 | √3 | 1/√3 | 2/√3 | 2 |
| 90° або π/2 радіан | 1 | 0 | ∞ | 0 | 1 | ∞ |
| 180° або π радіан | 0 | -1 | 0 | ∞ | ∞ | -1 |
| 270° або 3π/2 радіан | -1 | 0 | ∞ | 0 | -1 | ∞ |
| 360° або 2π радіан | 0 | 1 | 0 | ∞ | ∞ | 1 |
Переглянувши таблицю вище, ви помітите, що:
\(\mathbf{\sin x = \cos(90^\circ-x)}\) |
| \(\mathbf{\tan x = \cot(90^\circ-x)}\) |
| \(\mathbf{\sec x = \csc(90^\circ-x) }\) |
| \(\mathbf{\csc x = \sec(90^\circ-x)}\) |
| \( \mathbf{ \sin(-x) = -\sin x}\) |
| \( \mathbf{ \cos(-x) = \cos x}\) |
| \(\tan(-x) = -\tan x\) |
Графічне представлення \(\sin x\) і \(\cos x\) , де y змінюється від -1 до +1, коли x приймає значення від \(-3\pi \) до \(3\pi \) . Значення синуса та косинуса тригонометричної функції повторюються через інтервал \(2\pi \) .
Синус показано суцільною лінією, а косинус пунктирною лінією.
Розв’яжемо кілька прикладів на основі наведених вище тригонометричних функцій:
Приклад 1: якщо \(\cos x\) = − 4/5, x лежить у третьому квадранті, знайдіть значення інших п’яти тригонометричних функцій.
Рішення: зверніться до наведених вище таблиць.
Оскільки \(\cos x\) = -4/5, отже \(\sec x\) = -5/4
Оскільки \(\mathbf{ \cos^2 x + \sin^2x = 1}\) то \({16\over25} + \sin^2x = 1 ⇒ \sin^2x = 1-\frac{16}{25} = {9\over25}\)
\(\sin x = \pm3/5\)
Оскільки x лежить у значенні третього квадранта, тому \(\sin x\) буде від'ємним (див. таблицю знаків квадранта). Тому \(\sin x\) = -3/5 і \(\csc x \) = -5/3
Оскільки \(\tan x = \sin x/\cos x\) , то \(\tan x\) = \(\frac{-4/5}{-3/5}\) = 4/3
Приклад 2. Знайдіть значення \(\cos(5\pi/2)\)
рішення: \(\cos(5\pi/2) = \cos (2\pi + {1\pi}/_2)\)
Оскільки значення косинуса повторюється після \(2\pi \) , отже \(\cos(2\pi + {1\pi}/_2) = \cos(\pi/2) = 0\)