جیسا کہ ہم جانتے ہیں کہ دائیں مثلث کے لیے ایک شدید زاویہ کو اس کے اطراف کے تناسب کے طور پر کیسے ناپنا ہے، یہ وقت ہے کہ ریڈین پیمائش کے لحاظ سے کسی بھی زاویہ کے مثلثی تناسب کو سیکھیں اور ان کا مثلثی افعال کے طور پر مطالعہ کریں۔
یونٹ رداس کے ایک دائرے پر غور کریں، جس کا مرکز محور محور کی اصل پر ہے۔
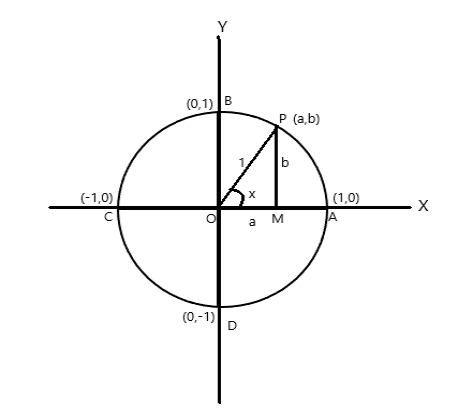
A = (1,0)، B = (0،1)، C = (-1،0) اور D = (0،-1) کے کوآرڈینیٹ پوائنٹس
P (a,b) کو \(\angle AOP = x \) ریڈین کے ساتھ دائرے پر کوئی بھی نقطہ ہونے دیں۔ لہذا قوس کی لمبائی \(AP = x \) یونٹ۔
\(\cos x = a\) , \(\sin x = b\) ۔ جیسا کہ \(\bigtriangleup POM\) ایک دائیں زاویہ مثلث ہے، \(OP^2 = OM^2 + PM^2\)
لہذا \(1 = a^2 + b^2\)
| \(\mathbf{ \cos^2 x + \sin^2x = 1}\) |
چونکہ ایک مکمل انقلاب دائرے کے مرکز میں \(2\pi\) ریڈین کا زاویہ بناتا ہے۔ مندرجہ بالا اعداد و شمار سے
\(\angle AOB = \pi/2 \)
\(\angle AOC = \pi\)
\(\angle AOD = \frac{3\pi}{2} \)
ہم جانتے \(\cos x = \frac {\textrm {Base}}{\textrm{Hypotenuse}}\) اور \(\sin x = \frac {\textrm {Perpendicular}}{\textrm{Hypotenuse}}\)
\(\cos0^\circ = 1\) \(\sin0^\circ = 0\)
\(\cos\frac{\pi}{2} = 0\) \(\sin\frac{\pi}{2} = 1\)
\(\cos\pi = -1\) \(\sin\pi = 0\)
\(\cos2\pi = 1\) \(\sin2\pi = 0\)
جب ہم پوائنٹ P سے ایک مکمل انقلاب لیتے ہیں تو ہم دوبارہ پوائنٹ P تک پہنچ جاتے ہیں \(\cos x\) اور \(\sin x\) کی قدر ایک جیسی رہتی ہے، اس لیے ہم کہہ سکتے ہیں کہ
جیسا کہ x \ \(2\pi\) کے اٹوٹ ملٹیپل سے بڑھتا یا گھٹتا ہے، سائن، کوزائن فنکشن کی قدر تبدیل نہیں ہوتی ہے۔ اس طرح،
\(\sin(n\cdot2\pi + x) = \sin x\)
\(\cos(n\cdot 2\pi + x) = \cos x \)
جہاں n ایک عدد عدد ہے۔
ہم دیکھیں گے کہ \(\sin x = 0\) جب \(\space x = n\pi\)
اور \(\cos x = 0\) جب \(x = (2n+1)\pi/2\)
sine اور cosine کے افعال کے لحاظ سے دیگر trigonometric افعال اخذ کرنا۔
| \(\mathbf{\csc x} = \mathbf{\frac{1}{\sin x}}\) جہاں \(x \neq n\pi\) |
| \(\mathbf{\sec x } = \mathbf{\frac{1}{\cos x}}\) جہاں |
| \(\mathbf{\tan x } = \mathbf{\frac{\sin x}{\cos x}}\) جہاں |
| \(\mathbf{\cot x } = \mathbf{\frac{\cos x}{\sin x}}\) جہاں \( x \neq n\pi\) |
| \(\textbf 1 + \mathbf {\tan^2x = \sec^2x}\) |
| \(\textbf 1 + \mathbf {\cot^2x = \csc^2x}\) |
نیچے دی گئی جدول سے پتہ چلتا ہے کہ مختلف کواڈرینٹ میں مثلثی افعال کی نشانی اور قدر کیسے بدلتی ہے۔
| چوکور | میں | II | III | چہارم |
| sinx | + | + | - | - |
| cosx | + | - | - | + |
| ٹینکس | + | - | + | - |
| cosecx | + | + | - | - |
| سیکس | + | - | - | + |
| cotx | + | - | + | - |
نیچے دیے گئے جدول پر ایک نظر ڈالیں جو 0°، 30°، 45°، 60°، اور 90° جیسی ڈگریوں کے لیے مثلثی زاویوں کی قدر کو ظاہر کرتا ہے۔
زاویے (ڈگری اور ریڈین میں) | گناہ | cos | ٹین | پلنگ | csc | سیکنڈ |
| 0° | 0 | 1 | 0 | ∞ | ∞ | 1 |
| 30° یا π/6 ریڈین | 1/2 | √3/2 | 1/√3 | √3 | 2 | 2/√3 |
| 45° یا π/4 ریڈین | 1/√2 | 1/√2 | 1 | 1 | √2 | √2 |
| 60° یا π/3 ریڈین | √3/2 | 1/2 | √3 | 1/√3 | 2/√3 | 2 |
| 90° یا π/2 ریڈین | 1 | 0 | ∞ | 0 | 1 | ∞ |
| 180° یا π ریڈین | 0 | -1 | 0 | ∞ | ∞ | -1 |
| 270° یا 3π/2 ریڈین | -1 | 0 | ∞ | 0 | -1 | ∞ |
| 360° یا 2π ریڈین | 0 | 1 | 0 | ∞ | ∞ | 1 |
مندرجہ بالا جدول کا مشاہدہ کریں، آپ دیکھیں گے کہ:
\(\mathbf{\sin x = \cos(90^\circ-x)}\) |
| \(\mathbf{\tan x = \cot(90^\circ-x)}\) |
| \(\mathbf{\sec x = \csc(90^\circ-x) }\) |
| \(\mathbf{\csc x = \sec(90^\circ-x)}\) |
| \( \mathbf{ \sin(-x) = -\sin x}\) |
| \( \mathbf{ \cos(-x) = \cos x}\) |
| \(\tan(-x) = -\tan x\) |
\(\sin x\) اور \(\cos x\) کی گرافیکل نمائندگی جہاں y کی حد -1 سے +1 تک ہوتی ہے جب x اقدار کو \(-3\pi \) سے \(3\pi \) تک لیتا ہے۔ مثلث فنکشن سائن اور کوسائن دونوں قدریں \(2\pi \) کے وقفہ کے بعد دہرائی جاتی ہیں۔
سائن کو ٹھوس لائن کے طور پر اور کوزائن کو نقطے والی لائن کے طور پر دکھایا گیا ہے۔
آئیے مندرجہ بالا مثلثی افعال کی بنیاد پر چند مثالوں کو حل کرتے ہیں:
مثال 1: اگر \(\cos x\) = − 4/5، x تیسرے کواڈرینٹ میں ہے، تو دیگر پانچ مثلثی افعال کی قدریں تلاش کریں۔
حل: اوپر دی گئی جدولوں کو دیکھیں۔
جیسا کہ \(\cos x\) = -4/5، لہذا \(\sec x\) = -5/4
جیسا کہ \(\mathbf{ \cos^2 x + \sin^2x = 1}\) تو \({16\over25} + \sin^2x = 1 ⇒ \sin^2x = 1-\frac{16}{25} = {9\over25}\)
\(\sin x = \pm3/5\)
چونکہ x تیسرے کواڈرینٹ قدر میں ہے، اس لیے \(\sin x\) منفی ہو گا (کواڈرینٹ سائن ٹیبل سے رجوع کریں)۔ لہذا \(\sin x\) = -3/5 اور \(\csc x \) = -5/3
جیسا کہ \(\tan x = \sin x/\cos x\) ، لہذا \(\tan x\) = \(\frac{-4/5}{-3/5}\) = 4/3
مثال 2: \(\cos(5\pi/2)\) کی قدر تلاش کریں
حل: \(\cos(5\pi/2) = \cos (2\pi + {1\pi}/_2)\)
چونکہ کوزائن کی قدر \(2\pi \) کے بعد دہرائی جاتی ہے لہذا \(\cos(2\pi + {1\pi}/_2) = \cos(\pi/2) = 0\)