To'g'ri burchakli uchburchak uchun o'tkir burchakni uning tomonlari nisbati sifatida qanday o'lchashni bilganimizdek, radian o'lchovi nuqtai nazaridan istalgan burchakka trigonometrik nisbatlarni o'rganish va ularni trigonometrik funktsiyalar sifatida o'rganish vaqti keldi.
Markazi koordinata o'qlari boshida joylashgan birlik radiusi doirasini ko'rib chiqaylik.
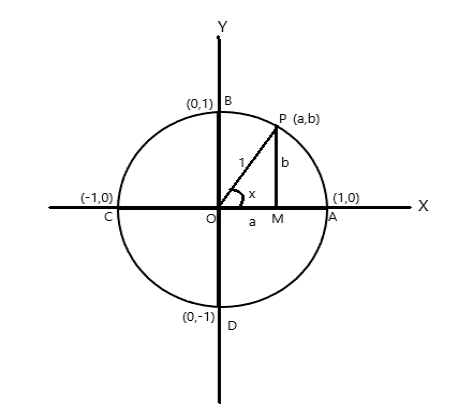
A = (1,0), B = (0,1), C = (-1,0) va D = (0,-1) koordinata nuqtalari
P (a,b) aylananing \(\angle AOP = x \) radianli istalgan nuqtasi bo'lsin. Shuning uchun yoy uzunligi \(AP = x \) birligi.
\(\cos x = a\) , \(\sin x = b\) . \(\bigtriangleup POM\) toʻgʻri burchakli uchburchak boʻlgani uchun \(OP^2 = OM^2 + PM^2\)
shuning uchun \(1 = a^2 + b^2\)
| \(\mathbf{ \cos^2 x + \sin^2x = 1}\) |
Bitta to'liq aylanish doiraning markazida \(2\pi\) radian burchak ostida bo'lgani uchun. Yuqoridagi rasmdan
\(\angle AOB = \pi/2 \)
\(\angle AOC = \pi\)
\(\angle AOD = \frac{3\pi}{2} \)
Biz \(\cos x = \frac {\textrm {Base}}{\textrm{Gipotenuza}}\) va \(\sin x = \frac {\textrm {Perpendicular}}{\textrm{Gipotenuza}}\)
\(\cos0^\circ = 1\) \(\sin0^\circ = 0\)
\(\cos\frac{\pi}{2} = 0\) \(\sin\frac{\pi}{2} = 1\)
\(\cos\pi = -1\) \(\sin\pi = 0\)
\(\cos2\pi = 1\) \(\sin2\pi = 0\)
P nuqtadan bir marta to'liq inqilob qilsak, yana P nuqtaga erishamiz \(\cos x\) va \(\sin x\) qiymati bir xil bo'lib qoladi, shuning uchun aytishimiz mumkinki,
x ning integral karrali \(2\pi\) ga ortishi yoki kamayishi bilan sinus, kosinus funksiyasi qiymati o'zgarmaydi. Shunday qilib,
\(\sin(n\cdot2\pi + x) = \sin x\)
\(\cos(n\cdot 2\pi + x) = \cos x \)
bu yerda n butun son.
Biz \(\sin x = 0\) qachon \(\space x = n\pi\) ekanligini sezamiz.
va \(\cos x = 0\) qachon \(x = (2n+1)\pi/2\)
Boshqa trigonometrik funktsiyalarni sinus va kosinus funktsiyalari bo'yicha chiqarish.
| \(\mathbf{\csc x} = \mathbf{\frac{1}{\sin x}}\) bu erda \(x \neq n\pi\) |
| \(\mathbf{\sec x } = \mathbf{\frac{1}{\cos x}}\) bu erda |
| \(\mathbf{\tan x } = \mathbf{\frac{\sin x}{\cos x}}\) bu erda |
| \(\mathbf{\cot x } = \mathbf{\frac{\cos x}{\sin x}}\) bu erda \( x \neq n\pi\) |
| \(\textbf 1 + \mathbf {\tan^2x = \sec^2x}\) |
| \(\textbf 1 + \mathbf {\cot^2x = \csc^2x}\) |
Quyidagi jadvalda trigonometrik funksiyalarning belgisi va qiymati turli kvadrantlarda qanday o'zgarishi ko'rsatilgan.
| Kvadrantlar | I | II | III | IV |
| sinx | + | + | − | − |
| cosx | + | − | − | + |
| tanx | + | − | + | − |
| kosekx | + | + | − | − |
| sekx | + | − | − | + |
| cotx | + | − | + | − |
0°, 30°, 45°, 60° va 90° kabi darajalar uchun trigonometrik burchaklar qiymatini koʻrsatadigan quyidagi jadvalga qarang.
Burchaklar (gradus va radianda) | sin | cos | tan | cot | csc | sek | |
| 0° | 0 | 1 | 0 | ∞ | ∞ | 1 | |
| 30° yoki p/6 radian | 1/2 | √3/2 | 1/√3 | √3 | 2 | 2/√3 | |
| 45 ° yoki p/4 radian | 1/√2 | 1/√2 | 1 | 1 | √2 | √2 | |
| 60° yoki p/3 radian | √3/2 | 1/2 | √3 | 1/ √3 | 2/√3 | 2 | |
| 90° yoki p/2 radian | 1 | 0 | ∞ | 0 | 1 | ∞ | |
| 180° yoki p radian | 0 | -1 | 0 | ∞ | ∞ | -1 | |
| 270 | ° yoki 3p/2 radian | -1 | 0 | ∞0 | - | 1 | ∞ |
| 360° yoki 2p radian | 0 | 1 | 0 | ∞ | ∞ | 1 |
Yuqoridagi jadvalga e'tibor bering, shuni ko'rasiz:
(\mathbf{\tan x = \cot(90^\circ)\(\mathbf{\sin x = \cos(90^\circ-x)}\) |
| \(\mathbf{\tan x = \cot(90^\circ-x)}\) |
| \(\mathbf{\tan x = \cot(90^\circ-x)}\) |
| \(\mathbf{\sec x = \csc(90^\circ-x) }\) |
| \(\mathbf{\csc x = \sec(90^\circ-x)}\) |
| \( \mathbf{ \sin(-x) = -\sin x}\) |
| \( \mathbf{ \cos(-x) = \cos x}\) |
| \(\tan(-x) = -\tan x\) |
\(\sin x\) va \(\cos x\) ning grafik tasviri, bunda y -1 dan +1 gacha, x \(-3\pi \) dan \(3\pi \) gacha boʻlgan qiymatlarni oladi. . Trigonometrik funktsiyaning sinus va kosinus qiymatlari \(2\pi \) oraliqdan keyin takrorlanadi.
Sinus qattiq chiziq, kosinus esa nuqtali chiziq sifatida ko'rsatilgan.
Keling, yuqoridagi trigonometrik funktsiyalarga asoslanib, bir nechta misollarni hal qilaylik:
1-misol: Agar \(\cos x\) = − 4/5, x uchinchi kvadrantda yotsa, qolgan beshta trigonometrik funktsiyaning qiymatlarini toping.
Yechim: Yuqorida keltirilgan jadvallarga qarang.
Sifatida \(\cos x\) = -4/5, shuning uchun \(\sec x\) = -5/4
\(\mathbf{ \cos^2 x + \sin^2x = 1}\) kabi \({16\over25} + \sin^2x = 1 ⇒ \sin^2x = 1-\frac{16}{25} = {9\over25}\)
\(\sin x = \pm3/5\)
X uchinchi kvadrant qiymatida joylashgani uchun \(\sin x\) manfiy bo'ladi (kvadrant belgilari jadvaliga qarang). Shuning uchun \(\sin x\) = -3/5 va \(\csc x \) = -5/3
Sifatida \(\tan x = \sin x/\cos x\) , shuning uchun \(\tan x\) = \(\frac{-4/5}{-3/5}\) = 4/3
2-misol : \(\cos(5\pi/2)\) qiymatini toping
Yechim: \(\cos(5\pi/2) = \cos (2\pi + {1\pi}/_2)\)
Kosinus qiymati \(2\pi \) dan keyin takrorlanganidek, \(\cos(2\pi + {1\pi}/_2) = \cos(\pi/2) = 0\)